某新型高科技商品，每件的售價比進價多6元，5件的進價相當于4件的售價，每天可售出200件，經市場調查發現，如果每件商品漲價1元，每天就會少賣5件．
（1）該商品的售價和進價分別是多少元？
（2）設每天的銷售利潤為w元，每件商品漲價a元，則當售價為多少元時，該商品每天的銷售利潤最大，最大利潤為多少元？
【考點】二次函數的應用．
【答案】（1）該商品每件的售價為30元，進價為每件24元；
（2）當售價為47元時，該商品每天的銷售利潤最大，最大利潤為2645元．
（2）當售價為47元時，該商品每天的銷售利潤最大，最大利潤為2645元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/23 22:30:2組卷：1911引用：5難度：0.5
相似題
-
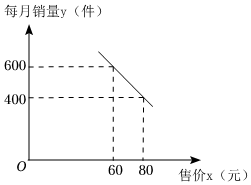1．某商家準備銷售一種防護品，進貨價格為每件50元，并且每件的售價不低于進貨價．經過市場調查，每月的銷售量y（件）與每件的售價x（元）之間滿足如圖所示的函數關系．
（1）求每月的銷售量y（件）與每件的售價x（元）之間的函數關系式；（不必寫出自變量的取值范圍）
（2）物價部門規定，該防護品每件的利潤不允許高于進貨價的30%．設這種防護品每月的總利潤為w（元），那么售價定為多少元可獲得最大利潤？最大利潤是多少？發布：2025/5/24 6:0:2組卷：3641引用：11難度：0.4 -
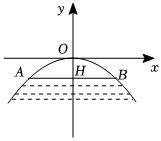2．如圖所示，拱橋的形狀是拋物線，其函數關系式為，當水面離橋頂的高度OH為4m時，水面的寬度AB為 m.y=-116x2發布：2025/5/24 6:0:2組卷：234引用：3難度：0.7 -
3．為了節省材料，某水產養殖戶利用水庫的岸堤（岸堤足夠長）為一邊，用總長為160m的圍網在水庫中圍成了如圖所示的①②③三塊矩形區域，而且這三塊矩形區域的面積相等．設BC的長度為xm,矩形區域ABCD的面積為ym2
（1）是否存在x的值，使得矩形ABCD的面積是1500m2；
（2）x為何值時，y有最大值？最大值是多少？發布：2025/5/24 5:0:1組卷：1245引用：6難度：0.4