如圖1，在矩形ABCD中，AD=24，P是邊BC邊上一動點，把△PCD沿直線PD折疊，頂點C的對應點是點G，DG交AB于點F，PG交AB于點E，連結CF交DP于點M，且CF∥PG．
（1）求證：△DAF∽△FBC；
（2）如圖1，當DC=50，且AF＞BF時，求tan∠CDP的值；
（3）如圖2，當CP=18時，求CF?FM的值．
【考點】相似形綜合題．
【答案】（1）證明見解答過程；
（2）tan∠CDP的值為；
（3）CF?FM的值是432．
（2）tan∠CDP的值為
1
3
（3）CF?FM的值是432．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：60引用：1難度：0.1
相似題
-
1．【問題探究】如圖1，在正方形ABCD中，點E、F分別在邊DC、BC上，且AE⊥DF，求證：AE=DF．
【知識遷移】如圖2，在矩形ABCD中，AB=3，BC=4，點E在邊AD上，點M、N分別在邊AB、CD上，且BE⊥MN，求的值．BEMN
【拓展應用】如圖3，在平行四邊形ABCD中，AB=m,BC=n,點E、F分別在邊AD、BC上，點M、N分別在邊AB、CD上，當∠EFC與∠MNC的度數之間滿足什么數量關系時，有試寫出其數量關系，并說明理由．EFMN=mn？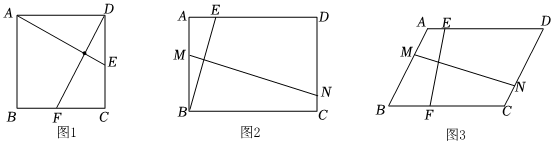
發布：2025/5/23 12:30:2組卷：746引用：1難度：0.4 -
2．綜合與實踐
【問題情境】
數學活動課上，楊老師出示了教材上的一個問題：
如圖1，四邊形ABCD是正方形，G是BC上的任意一點，DE⊥AG于點E，BF∥DE，交AG于點F，求證：AF-BF=EF．
數學興趣小組的小明同學做出了回答，解題思路如下：
由正方形的性質得到AB=AD，∠BAD=90°，
再由垂直和平行可知∠AED=∠AFB=90°，
再利用同角的余角相等得到∠ADE=∠BAF，
則可根據“AAS”判定△ADE≌△BAF，
得到AE=BF，所以AF-BF=AF-AE=EF．
【建立模型】
該數學小組小芳同學受此問題啟發，對上面的問題進行了改編，并提出了如下問題：
（1）如圖2，四邊形ABCD是正方形，E，F是對角線AC上的點，BF∥DE，連接BE，DF．
求證：四邊形BEDF是菱形；
【模型拓展】
該興趣小組的同學們在楊老師的指導下大膽嘗試，改變圖形模型，發現并提出新的探究點；
（2）如圖3，若正方形ABCD的邊長為12，E是對角線AC上的一點，過點E作EG⊥DE，交邊BC于點G，連接DG，交對角線AC于點F，CF：EF=3：5，求FG?DF的值．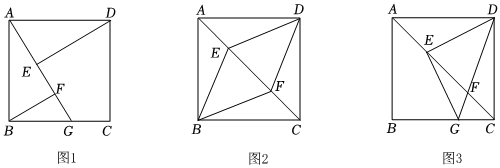
發布：2025/5/23 12:30:2組卷：676引用：1難度：0.4 -
3．已知點E、F分別是四邊形ABCD邊AB、AD上的點，且DE與CF相交于點G．
（1）如圖①，若AB∥CD，AB=CD，∠A=90°，且AD?DF=AE?DC，求證：∠CGE=90°；
（2）如圖②，若AB∥CD，AB=CD，且∠A=∠EGC時，求證：DE?CD=CF?DA；
（3）如圖③，若BA=BC=3，DA=DC=4，設DE⊥CF，當∠BAD=90°時，直接寫出的值．DECF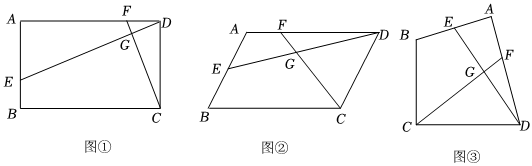
發布：2025/5/23 13:30:1組卷：556引用：2難度：0.3