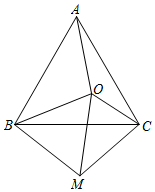
 如圖,點O為等邊三角形ABC內一點,連接OA,OB,OC,將線段BO繞點B順時針旋轉60°到BM,連接CM,OM.
如圖,點O為等邊三角形ABC內一點,連接OA,OB,OC,將線段BO繞點B順時針旋轉60°到BM,連接CM,OM.
(1)求證:AO=CM;
(2)若OA=8,OC=6,OB=10,判斷△OMC的形狀并證明.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/21 8:0:9組卷:1482引用:14難度:0.5
相似題
-
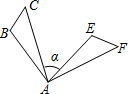 1.如圖,△ABC繞點A順時針旋轉80°得到△AEF,若∠B=100°,∠F=50°,則∠α的度數是.發布:2025/7/1 13:0:6組卷:1099引用:19難度:0.7
1.如圖,△ABC繞點A順時針旋轉80°得到△AEF,若∠B=100°,∠F=50°,則∠α的度數是.發布:2025/7/1 13:0:6組卷:1099引用:19難度:0.7 -
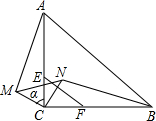 2.如圖,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分別是CA,CB邊的三等分點,將△ECF繞點C逆時針旋轉α角(0°<α<90°),得到△MCN,連接AM,BN.
2.如圖,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分別是CA,CB邊的三等分點,將△ECF繞點C逆時針旋轉α角(0°<α<90°),得到△MCN,連接AM,BN.
(1)求證:AM=BN;
(2)當MA∥CN時,試求旋轉角α的余弦值.發布:2025/6/25 6:30:1組卷:2475引用:59難度:0.5 -
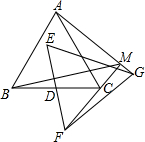 3.如圖,△ABC,△EFG均是邊長為2的等邊三角形,點D是邊BC、EF的中點,直線AG、FC相交于點M.當△EFG繞點D旋轉時,線段BM長的最小值是( )
3.如圖,△ABC,△EFG均是邊長為2的等邊三角形,點D是邊BC、EF的中點,直線AG、FC相交于點M.當△EFG繞點D旋轉時,線段BM長的最小值是( )A.2- 3B. +13C. 2D. -13發布:2025/6/25 6:0:1組卷:5914引用:58難度:0.5


