下面是王倩同學(xué)的作業(yè)及自主探究筆記，請認(rèn)真閱讀并補(bǔ)充完整．
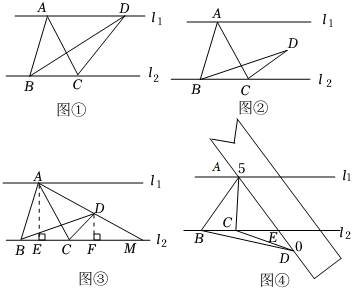
【作業(yè)】如圖①，直線l1∥l2，△ABC與△DBC的面積相等嗎？為什么？
解：相等．理由如下：
設(shè)l1與l2之間的距離為h,
則S△ABC=12BC?h,S△DBC=12BC?h.
∴S△ABC=S△DBC．
【探究】（1）如圖②，當(dāng)點(diǎn)D在l1，l2之間時(shí)，設(shè)點(diǎn)A，D到直線l2的距離分別為h,h′，則S△ABCS△DBC=hh′．
證明：∵S△ABC=12BC?h12BC?h．
（2）如圖③，當(dāng)點(diǎn)D在l1，l2之間時(shí)，連接AD并延長交l2于點(diǎn)M，則S△ABCS△DBC=AMDM．
證明：過點(diǎn)A作AE⊥BM，垂足為E，過點(diǎn)D作DF⊥BM，垂足為F，則∠AEM=∠DFM=90°．
∴AE∥DFDF．
∴△AEM∽△DFM△DFM．
∴AEDF=AMDM．
由【探究】（1）可知S△ABCS△DBC=AEDFAEDF，
∴S△ABCS△DBC=AMDM．
（3）如圖④，當(dāng)點(diǎn)D在l2下方時(shí)，連接AD交l2于點(diǎn)E．若點(diǎn)A，E，D所對應(yīng)的刻度值分別為5，1.5，0，則S△ABCS△DBC的值為 7373．
1
2
1
2
S
△
ABC
S
△
DBC
h
h
′
1
2
1
2
S
△
ABC
S
△
DBC
AM
DM
AE
DF
AM
DM
S
△
ABC
S
△
DBC
AE
DF
AE
DF
S
△
ABC
S
△
DBC
AM
DM
S
△
ABC
S
△
DBC
7
3
7
3
【考點(diǎn)】相似形綜合題．
【答案】BC?h；DF；△DFM；；
1
2
AE
DF
7
3
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：963引用：4難度：0.5
相似題
-
1．在Rt△ABC中，∠ACB=90°，tan∠ABC=a,D是BC上一點(diǎn)（不與點(diǎn)B，C重合），連接AD，過點(diǎn)C作CE⊥AD于點(diǎn)E，連接BE并延長，交AC于點(diǎn)F．
（1）如圖1，當(dāng)a=1時(shí)，
①求證：∠ECD＜45°；
②求證：；BEEF=CDCF
（2）如圖2，若D是BC的中點(diǎn)，求tan∠CEF的值（用含a的代數(shù)式表示）．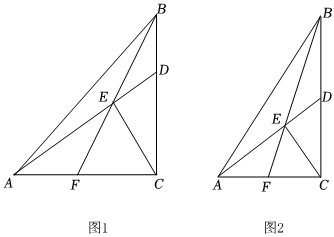
發(fā)布：2025/6/5 6:0:2組卷：335引用：4難度：0.3 -
2．綜合與實(shí)踐
我們在沒有量角器或三角尺的情況下，用折疊特殊矩形紙片的方法進(jìn)行如下操作也可以得到幾個(gè)相似的含有30°角的直角三角形．
實(shí)踐操作：
第一步：如圖①，矩形紙片ABCD的邊長AB=，將矩形紙片ABCD對折，使點(diǎn)D與點(diǎn)A重合，點(diǎn)C與點(diǎn)B重合，折痕為EF，然后展開，EF與CA交于點(diǎn)H．5
第二步：如圖②，將矩形紙片ABCD沿過點(diǎn)C的直線再次折疊，使CD落在對角線CA上，點(diǎn)D的對應(yīng)點(diǎn)D'恰好與點(diǎn)H重合，折痕為CG，將矩形紙片展平，連接GH．
問題解決：
（1）在圖②中，sin∠ACB=，=；EGCG
（2）在圖②中，CH2=CG?；從圖②中選擇一條線段填在空白處，并證明你的結(jié)論；
拓展延伸：
（3）將上面的矩形紙片ABCD沿過點(diǎn)C的直線折疊，點(diǎn)D的對應(yīng)點(diǎn)D′落在矩形的內(nèi)部或一邊上，設(shè)∠DCD′=α，若0°＜α≤90°，連接D′A，D′A的長度為m,則m的取值范圍是 ．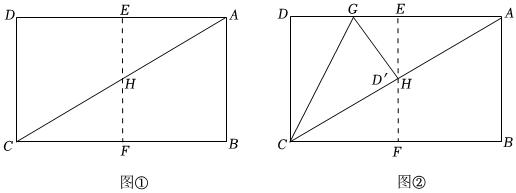
發(fā)布：2025/6/5 1:30:2組卷：279引用：2難度：0.2 -
3．（1）如圖所示，矩形ABCD中，BC=2AB，將矩形ABCD繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)90°，得到新的矩形BEFH，連接FD，EC，線段EC交FD于點(diǎn)G，連BG．
①請直接寫出線段FB和BD的數(shù)量關(guān)系 ，位置關(guān)系 ；
②求證：FD=2BG．
（2）如圖2所示，Rt△BCD中，∠C=90°，BC=3CD，將Rt△BCD繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)α°，得到新的Rt△BEF，連接EC，F(xiàn)D，線段EC，F(xiàn)D相交于點(diǎn)G，點(diǎn)O為線段BD中點(diǎn)，連OG，在Rt△BCD旋轉(zhuǎn)的過程中，是否發(fā)生改變？如果不變，請求出OGBC的值；如果發(fā)生改變，請說明理由．OGBC發(fā)布：2025/6/5 7:30:1組卷：455引用：5難度：0.1