圖1是某型號挖掘機，該挖掘機是由基座、主臂和伸展臂構成．圖2是某種工作狀態下的側面結構示意圖（MN是基座的高，MP是主臂，PQ是伸展臂，EM∥QN）．已知基座高度MN為1m,主臂MP長為5m,測得主臂伸展角．∠PME=37°．
（參考數據：sin37°≈35，tan37°≈34，sin53°≈45，tan53°≈43）
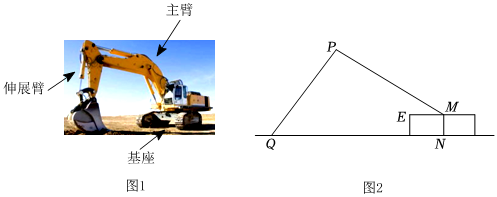
（1）求點P到地面的高度；
（2）若挖掘機能挖的最遠處點Q到點N的距離為7m,求∠QPM的度數．
3
5
3
4
4
5
4
3
【考點】解直角三角形的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 10:30:2組卷：2483引用：13難度：0.4
相似題
-
1．某數學興趣小組在探究如何求tan15°的值，經過思考、討論、交流，得到以下思路：思路一：如圖1，在Rt△ABC中，∠C=90°，∠ABC=30°，延長CB至點D，使BD=BA，連接AD．設AC=1，則BD=BA=2，BC=
．tanD=tan15°=3=12+3=2-2-3（2+3）（2-3）．思路二：利用科普書上的和（差）角正切公式：tan（α±β）=3．假設α=60°，β=45°代入差角正切公式：tan15°=tan（60°-45°）=tanα±tanβ1+tanαtanβ=tan60°-tan45°1+tan60°tan45°=2-3-11+3．請解決下列問題（上述思路僅供參考）．3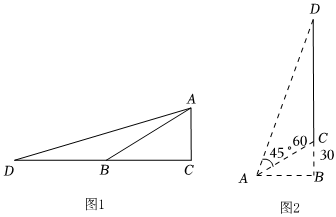
（1）類比：求出tan75°的值；
（2）應用：如圖2，某電視塔建在一座小山上，山高BC為30米，在地平面上有一點A，測得A，C兩點間距離為60米，從A測得電視塔的視角（∠CAD）為45°，求這座電視塔CD的高度．發布：2025/5/25 13:0:1組卷：142引用：2難度：0.4 -
2．如圖1是我們經常看到的一種折疊桌子，它是由下面的支架AD，BC與桌面構成如圖2，已知OA=OB=OC=OD=20
cm,∠COD=60°，則點A到地面（CD所在的平面）的距離是 cm.3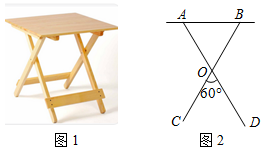
發布：2025/5/25 13:30:1組卷：188引用：4難度：0.6 -
3．如圖，某教學樓AB的后面有一建筑物CD，當光線與地面夾角是22°時，教學樓在建筑物的墻上留下高2米的影子CE；而當光線與地面夾角是45°時，教學樓頂A在地面上的影子F與墻角C有13米的距離（B、F、C在一條直線上），求教學樓AB的高度（sin22°≈，cos22°≈38，tan22°≈1516）25發布：2025/5/25 13:30:1組卷：1104引用：4難度：0.3