如圖，在四邊形ABCD中，對角線AC和BD相交于點E，且DA=DB=DC．
（1）求證：∠ADB=2∠ACB；
（2）如圖2，點F在BC邊上，AC與DF相交于點G，DE=BF，若∠BAC=30°，5CG=3DG，試探究AG與DG的數量關系，并說明理由；
（3）如圖3，在（2）的條件下，BN與DF相交于點M，若2∠BNC-2∠BFD=∠BCE，BC=7，求線段DM的長．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：202引用：2難度：0.3
相似題
-
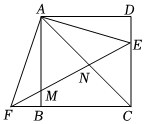1．如圖，在正方形ABCD中，點E是邊CD上的一點（不與點C，D重合），點F在邊CB的延長線上，且AE=AF，連接EF交AB于點M，交AC于點N．
（1）求證：AE⊥AF；
（2）若∠BAC=2∠BAF，求證：AF2=AMAB；?2
（3）若CE=nDE，求的值（用含n的式子表示）．FMAE發(fā)布：2025/5/30 22:30:1組卷：178引用：2難度：0.4 -
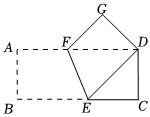2．如圖，將矩形ABCD（紙片）折疊，使點B與AD邊上的點D重合，EF為折痕．
（1）如果∠BEF=67.5°，那么∠CED=°；
（2）△DCE和△DGF正好關于某條直線成軸對稱．
①請在圖中畫出這條對稱軸；
②如果四邊形ABEF和四邊形CDFE關于EF的中點成中心對稱，且BE：CE=5：3，試求四邊形ABEF的面積與△DGF的面積的比值．發(fā)布：2025/5/30 20:0:1組卷：292引用：1難度：0.4 -
3．綜合與實踐圖形的幾何變換
復習課上，老師對一張平行四邊形紙片ABCD（AD＞AB）進行如下操作：
（1）如圖1，折疊該紙片，使邊AB恰好落在邊AD上，邊CD恰好落在邊CB上，得到折痕AE和CF，判斷四邊形AECF的形狀并說明理由；
（2）老師沿折痕將△ABE和△CDF剪下，得到兩個全等的等腰三角形，已知等腰三角形的腰長為5，底邊長為6，底角度數為α，通過不同的擺放方式，三個學習小組利用幾何變換設置了幾個問題，請一一解答．
①善思小組：
將兩個三角形擺放成如圖2的位置，使邊CF與邊EA重合，然后固定△ABE，將△CDF沿著射線EA的方向平移，如圖3，當四邊形FBED為矩形時，求平移的距離；
②勤學小組：
將兩個三角形擺成如圖4的位置，使△BAE與△DFC重合，取AE的中點O，固定△ABE，將△CDF繞著點O按逆時針方向旋轉（0°＜旋轉角＜360°），如圖5，在旋轉過程中，四邊形ACEF的形狀是 ．
③奮進小組：
在上面的旋轉過程中，利用圖6進行探究，當△BAE與△DFC的重疊部分為等腰三角形時，旋轉角為 （用含α的代數式表示），此時重疊部分的面積為 ．
發(fā)布：2025/5/30 23:30:1組卷：313引用：2難度：0.1