（1）如圖，P是正方形ABCD的BC邊上的中點(diǎn)，AP⊥PQ，且PQ交∠DCB的外角平分線于Q．求證：AP=PQ
（2）P是正方形ABCD的BC邊所在直線上的任一點(diǎn)，AP⊥PQ，且PQ交∠DCB的外角平分線所在直線于Q．（1）中的結(jié)論是否成立？試證之．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/26 16:0:1組卷：123引用：1難度：0.4
相似題
-
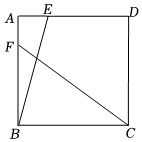1．在正方形ABCD中，AB=5，點(diǎn)E、F分別為AD、AB上一點(diǎn)，且AE=AF，連接BE、CF，則BE+CF的最小值是 ．發(fā)布：2025/6/4 21:30:2組卷：1570引用：5難度：0.3 -
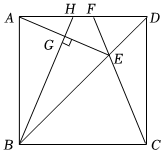2．如圖，在正方形ABCD中，E是對(duì)角線BD上一點(diǎn)，且滿足BE=BC，連接CE并延長(zhǎng)交AD于點(diǎn)F，連接AE，過(guò)B點(diǎn)作BG⊥AE于點(diǎn)G，延長(zhǎng)BG交AD于點(diǎn)H．在下列結(jié)論中：①AH=DF；②∠AEF=45°；③S四邊形EFGH=S△DEF+S△AGH；④△AED≌△CDE．其中正確的結(jié)論有 （填正確的序號(hào)）．發(fā)布：2025/6/4 22:30:1組卷：474引用：8難度：0.5 -
3．如圖，在?ABCD中，AD=2AB=2，∠ABC=60°，E，F(xiàn)是對(duì)角線BD上的動(dòng)點(diǎn)，且BE=DF，M，N分別是邊AD，邊BC上的動(dòng)點(diǎn)．下列四個(gè)結(jié)論：
①存在無(wú)數(shù)個(gè)平行四邊形MENF； ②存在無(wú)數(shù)個(gè)矩形MENF； ③存在無(wú)數(shù)個(gè)菱形MENF； ④存在兩個(gè)正方形MENF．其中正確的結(jié)論是 （填寫序號(hào)）．發(fā)布：2025/6/4 21:0:2組卷：231引用：3難度：0.4
相關(guān)試卷