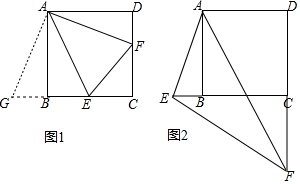
已知，如圖1，四邊形ABCD是正方形，E、F分別在邊BC、CD上，且∠EAF=45°，我們把這種模型稱為“半角模型”，在解決“半角模型”問題時，旋轉(zhuǎn)是一種常用的方法．
（1）在圖1中，連接EF，為了證明結(jié)論“EF=BE+DF”，小明將△ADF繞點A順時針旋轉(zhuǎn)90°后解答了這個問題，請按小明的思路寫出證明過程；
（2）如圖2，當(dāng)∠EAF的兩邊分別與CB、DC的延長線交于點E、F，連接EF，試探究線段EF、BE、DF之間的數(shù)量關(guān)系，并證明．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2152引用：3難度：0.3
相似題
-
1．如圖，在正方形ABCD中，點P是對角線BD上的一點，點E在AD的延長線上，且PA=PE，PE交CD于點F．
（1）證明：PC=PE；
（2）求∠CPE的度數(shù)．發(fā)布：2025/6/6 13:0:1組卷：533引用：7難度：0.6 -
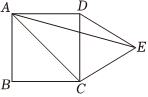
2．如圖，在正方形ABCD的外側(cè)，作等邊△DCE，則∠AEC的度數(shù)是 ．
發(fā)布：2025/6/6 14:0:1組卷：898引用：21難度：0.5 -
3．已知：P是正方形ABCD對角線BD上一點，PE⊥DC，PF⊥BC，E、F分別為垂足．
求證：AP=EF．發(fā)布：2025/6/6 12:30:1組卷：1350引用：25難度：0.6