已知：如圖，拋物線y=a（x-1）2+c與x軸交于點A（1-3，0）和點B，將拋物線沿x軸向上翻折，頂點P落在點P′（1，3）處．
（1）求原拋物線的解析式；
（2）學校舉行班徽設計比賽，九年級5班的小明在解答此題時頓生靈感：過點P′作x軸的平行線交拋物線于C、D兩點，將翻折后得到的新圖象在直線CD以上的部分去掉，設計成一個“W”型的班徽，“5”的拼音開頭字母為W，“W”圖案似大鵬展翅，寓意深遠；而且小明通過計算驚奇的發現這個“W”圖案的高與寬（CD）的比非常接近黃金分割比5-12（約等于0.618）．請你計算這個“W”圖案的高與寬的比到底是多少？（參考數據：5≈2.236，6≈2.449，結果可保留根號）
1
-
3
5
-
1
2
5
≈
2
.
236
6
≈
2
.
449
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：498引用：12難度：0.5
相似題
-
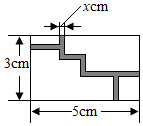1．如圖是一個迷宮游戲盤的局部平面簡化示意圖，該矩形的長、寬分別為5cm,3cm,其中陰影部分為迷宮中的擋板，設擋板的寬度為x cm,小球滾動的區域（空白區域）面積為y cm2，則下列所列方程正確的是（ ）發布：2025/6/7 8:30:2組卷：1587引用：8難度：0.6 -
2．我市某童裝專賣店在銷售中發現，一款童裝每件進價為40元，若銷售價為60元，每天可售出20件，為迎接“雙十一”，專賣店決定采取適當的降價措施，以擴大銷售量，經市場調查發現，如果每件童裝降價1元，那么平均可多售出2件．設每件童裝降價x元（x＞0）時，平均每天可盈利y元．
（1）寫出y與x的函數關系式；
（2）當該專賣店每件童裝降價多少元時，平均每天盈利400元？
（3）該專賣店要想平均每天盈利600元，可能嗎？請說明理由．發布：2025/6/6 21:0:2組卷：1167引用：7難度：0.5 -
3．從地面豎直向上拋出一小球，小球的高度h（單位；m）與小球的運動時間t（單位：s）之間的關系式是h=30t-5t2（0≤t≤6）．小球運動的時間是 s時，小球最高．
發布：2025/6/6 22:30:1組卷：243引用：1難度：0.6