如圖，在正方形ABCD中，E為AB邊上一點（不與點A，B重合），CF⊥DE于點G，交AD于點F，連接BG．
（1）求證：AE=DF；
（2）是否存在點E的位置，使得△BCG為等腰三角形？若存在，寫出一個滿足條件的點E的位置并證明；若不存在，說明理由．
【考點】正方形的性質；全等三角形的判定與性質．
【答案】（1）證明見解答；（2）存在，當點E為AB的中點時，△BCG為等腰三角形，理由見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1049引用：5難度：0.6
相似題
-
1．如圖，E、F分別是正方形ABCD的邊CD，AD上的點，且CE=DF，AE，BF相交于點O，下列結論①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四邊形DEOF中，正確結論的個數為（ ）發布：2025/6/17 15:30:1組卷：3091引用：25難度：0.7 -
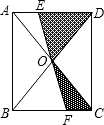2．如圖，已知面積為1的正方形ABCD的對角線相交于點O，過點O任意作一條直線分別交AD、BC于E、F，則陰影部分的面積是．發布：2025/6/17 14:30:2組卷：370引用：36難度：0.7 -
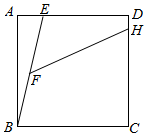3．如圖，正方形ABCD中，DE=2AE=4，F是BE的中點，點H在CD上，∠EFH=45°，則FH的長度為（ ）發布：2025/6/17 14:30:2組卷：825引用：3難度：0.4