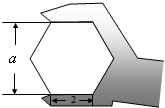
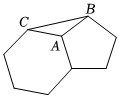
如圖,蜂巢的橫截面由正六邊形組成,且能無限無縫隙拼接,稱橫截面圖形由全等正多邊形組成,且能無限無縫隙拼接的多邊形具有同形結構.
如圖,蜂巢的橫截面由正六邊形組成,且能無限無縫隙拼接,稱橫截面圖形由全等正多邊形組成,且能無限無縫隙拼接的多邊形具有同形結構.
若已知具有同形結構的正n邊形的每個內角度數為α,滿足:360=kα(k為正整數),多邊形外角和為360°,則k關于邊數n的函數是k=2nn-2(n=3,4,6)或k=2+4n-2(n=3,4,6)k=2nn-2(n=3,4,6)或k=2+4n-2(n=3,4,6)(寫出n的取值范圍)
2
n
n
-
2
4
n
-
2
2
n
n
-
2
4
n
-
2
【答案】k=(n=3,4,6)或k=2+(n=3,4,6)
2
n
n
-
2
4
n
-
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:446引用:23難度:0.7