古希臘七賢之一，著名哲學(xué)家泰勒斯（Thales,公元前6世紀(jì)）最早從拼圖實踐中發(fā)現(xiàn)了“三角形內(nèi)角和等于180°”，但這種發(fā)現(xiàn)完全是經(jīng)驗性的，泰勒斯并沒有給出嚴(yán)格的證明．之后歐幾里得利用輔助平行線和延長線，通過一組同位角和內(nèi)錯角證明了該定理．請同學(xué)們幫助歐幾里得將證明過程補(bǔ)充完整．
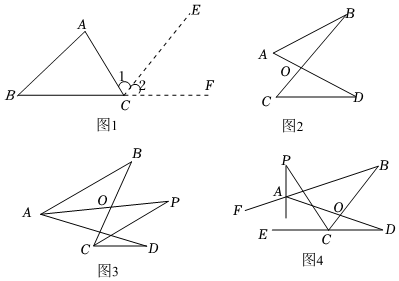
（1）已知：如圖1，在△ABC中，
求證：∠A+∠B+∠BCA=180°．
證明：延長線段BC至點F，并過點C作CE∥AB．
∵CE∥AB（已作），
∴∠A∠A=∠1（兩直線平行，內(nèi)錯角相等），
∠B∠B=∠2（兩直線平行，同位角相等）．
∵∠BCF=180°∠BCF=180°（平角的定義），
∴∠ACB+∠A+∠B=180°（等量代換）．
【實踐運用】
（2）如圖2，線段4D、BC相交于點O，連接AB、CD，試證明：∠A+∠B=∠C+∠D．
【拓展提升】
（3）①如圖3，AP、CP分別平分∠BAD、∠BCD，若∠ABC=34°，∠ADC=18°，則∠P的度數(shù)為 26°26°．
②如圖4，直線AP平分∠FAD，CP平分∠BCE，若∠ABC=34°，∠ADC=18°，則∠P的度數(shù)為 2626°．
【答案】∠A；∠B；∠BCF=180°；26°；26
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：80引用：1難度：0.6
相似題
-
1．如圖，△ABC中，D是AC上一點，過D作DE∥BC交AB于E點，F(xiàn)是BC上一點，連接DF．若∠1=∠AED．
（1）求證：DF∥AB．
（2）若∠1=55°，DF平分∠CDE，求∠C的度數(shù)．發(fā)布：2025/6/5 0:30:1組卷：898引用：7難度：0.7 -
2．如圖，AE與AD分別是△ABC的角平分線和高．若∠B=70°，∠C=60°，求∠DAE度數(shù)．發(fā)布：2025/6/5 0:30:1組卷：883引用：7難度：0.7 -
3．在一個三角形中，如果一個角是另一個角的3倍，這樣的三角形我們稱之為“靈動三角形”．例如，三個內(nèi)角分別為120°，40°，20°的三角形是“靈動三角形”．如圖∠MON=40°，在射線OM上找一點A，過點A作AB⊥OM交ON于點B，以A為端點作射線AD，交線段OB于點C（規(guī)定0°＜∠OAC＜60° ）．當(dāng)△ABC為“靈動三角形”時，∠OAC的度數(shù)為 ．發(fā)布：2025/6/4 23:30:1組卷：581引用：4難度：0.4