 我國南宋著名數學家秦九韶在他的著作《數書九章》中提出了“三斜求積術”,三斜即指三角形的三條邊長,可以用該方法求三角形面積.若改用現代數學語言表示,其形式為:設a,b,c為三角形三邊,S為面積,則S=14[a2b2-(a2+b2-c22)2]①
我國南宋著名數學家秦九韶在他的著作《數書九章》中提出了“三斜求積術”,三斜即指三角形的三條邊長,可以用該方法求三角形面積.若改用現代數學語言表示,其形式為:設a,b,c為三角形三邊,S為面積,則S=14[a2b2-(a2+b2-c22)2]①
這是中國古代數學的瑰寶之一.
而在文明古國古希臘,也有一個數學家海倫給出了求三角形面積的另一個公式,若設p=a+b+c2(周長的一半),則S=p(p-a)(p-b)(p-c)②
(1)嘗試驗證.這兩個公式在表面上形式很不一致,請你用以5,7,8為三邊構成的三角形,分別驗證它們的面積值;
(2)問題探究.經過驗證,你發現公式①和②等價嗎?若等價,請給出一個一般性推導過程(可以從①?②或者②?①);
(3)問題引申.三角形的面積是數學中非常重要的一個幾何度量值,很多數學家給出了不同形式的計算公式.請你證明如下這個公式:如圖,△ABC的內切圓半徑為r,三角形三邊長為a,b,c,仍記p=a+b+c2,S為三角形面積,則S=pr.
1
4
[
a
2
b
2
-
(
a
2
+
b
2
-
c
2
2
)
2
]
a
+
b
+
c
2
p
(
p
-
a
)
(
p
-
b
)
(
p
-
c
)
a
+
b
+
c
2
【考點】三角形的內切圓與內心;數學常識.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/17 17:0:2組卷:818引用:6難度:0.5
相似題
-
 1.如圖,在△ABC中,AC=BC,E是內心,AE的延長線交△ABC的外接圓于D.求證:
1.如圖,在△ABC中,AC=BC,E是內心,AE的延長線交△ABC的外接圓于D.求證:
(1)BE=AE;
(2).ABAC=AEED發布:2025/6/24 18:30:1組卷:99引用:1難度:0.5 -
2.若等腰直角三角形的外接圓半徑的長為2,則其內切圓半徑的長為( )
A. 2B.2 -22C.2- 2D. -22發布:2025/6/25 3:30:1組卷:2727引用:61難度:0.9 -
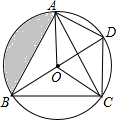 3.如圖,O是△ABC的內心,BO的延長線和△ABC的外接圓相交于點D,連接DC,DA,OA,OC,四邊形OADC為平行四邊形.
3.如圖,O是△ABC的內心,BO的延長線和△ABC的外接圓相交于點D,連接DC,DA,OA,OC,四邊形OADC為平行四邊形.
(1)求證:△BOC≌△CDA;
(2)若AB=2,求陰影部分的面積.發布:2025/6/24 11:30:1組卷:1586引用:51難度:0.5


