綜合與實踐
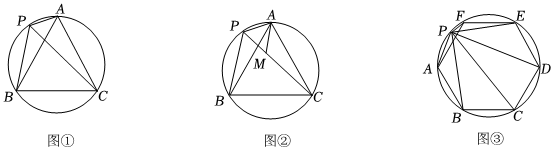
提出問題：在一次數學活動課的學習中，小明同學發現：“等邊三角形外接圓上任意一點到三個頂點的距離的平方和等于邊長平方的兩倍”．
（1）初步探究：如圖①，△ABC為等邊三角形，P是△ABC外接圓?AB上任意一點，證明PC=PA+PB的思路如下，圖②中，在PC上截取PM=PA，連接AM，先證明△PAM為等邊三角形，再證明△APB≌△AMC，由此得出PC=PA+PB．請寫出PC=PA+PB的證明過程．
（2）繼續探究：如圖②，設PA=x,PB=y,PC=z,AB=m.求證：x2+y2+z2=2m2．
（3）拓展探究：如圖③，點P為正六邊形ABCDEF的外接圓上一點，設PA=a,PB=b,PC=c,PD=d,PE=e,PF=f,AB=n.試探究a,b,c,d,e,f與n之間的數量關系．
?
AB
【考點】圓的綜合題．
【答案】（1）見解析；
（2）見解析；
（3）a2+c2+e2+b2+d2+f2=12n2．
（2）見解析；
（3）a2+c2+e2+b2+d2+f2=12n2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：109引用：1難度：0.2
相似題
-
1．如圖，AB是圓O的直徑，弦CD與AB交于點H，∠BDC=∠CBE．
（1）求證：BE是圓O的切線；
（2）若CD⊥AB，AC=2，BH=3，求劣弧BC的長；
（3）如圖，若CD∥BE，作DF∥BC，滿足BC=2DF，連接FH、BF，求證：FH=BF．發布：2025/1/28 8:0:2組卷：100引用：1難度：0.1 -
2．如圖，AB是圓O的直徑，AB=6，D是半圓ADB上的一點，C是弧BD的中點．
（1）若∠ABD=30°，求BC的長和由弦BC、BD、和弧CD圍成的圖形面積；
（2）若弧AD的度數是120度，在半徑OB上是否存在點P，使得PC+PD的值最小，如果存在，請在備用圖中畫出P的位置，并求PC+PD的最小值，如果不存在，請說明理由．
發布：2025/1/28 8:0:2組卷：44引用：0難度：0.3 -
3．如圖，AB是圓O的直徑，弦CD⊥AB于G，射線DO與直線CE相交于點E，直線DB與CE交于點H，且∠BDC=∠BCH．
（1）求證：直線CE是圓O的切線．
（2）如圖1，若OG=BG，BH=1，直接寫出圓O的半徑；
（3）如圖2，在（2）的條件下，將射線DO繞D點逆時針旋轉，得射線DM，DM與AB交于點M，與圓O及切線CF分別相交于點N，F，當GM=GD時，求切線CF的長．
發布：2025/1/28 8:0:2組卷：782引用：2難度：0.1