《見微知著》談到:從一個簡單的經典問題出發,從特殊到一般,由簡單到復雜:從部分到整體,由低維到高維,知識與方法上的類比是探索發展的重要途徑,是思想閥門發現新問題、新結論的重要方法.
閱讀材料一:
利用整體思想解題,運用代數式的恒等變形,使不少依照常規思路難以解決的問題找到簡便解決方法,常用的途徑有:(1)整體觀察;(2)整體設元;(3)整體代入;(4)整體求和等.
例如,ab=1求證:11+a+11+b=1
證明:原式=abab+a+11+b=b1+b+11+b=1
波利亞在《怎樣解題》中指出:“當你找到第一個藤菇或作出第一個發現后,再四處看看,他們總是成群生長”類似問題,我們有更多的式子滿足以上特征.
閱讀材料二:
基本不等式ab≤a+b2(a>0,b>0),當且僅當a=b時等號成立,它是解決最值問題的有力工具.
例如:在x>0的條件下,當x為何值時,x+1x有最小值,最小值是多少?
解:∵x>0,1x>0∴x+1x2≥x?1x,即x+1x≥2x?1x,∴x+1x≥2
當且僅當x=1x,即x=1時,x+1x有最小值,最小值為2.
請根據閱讀材料解答下列問題:
(1)已知ab=1,求下列各式的值:
①11+a2+11+b2=11;
②11+an+11+bn=11.
(2)若abc=1,解方程5axab+a+1+5bxbc+b+1+5cxca+c+1=1
(3)若正數a、b滿足ab=1,求M=11+a+11+2b的最小值.
1
1
+
a
+
1
1
+
b
ab
ab
+
a
+
1
1
+
b
b
1
+
b
+
1
1
+
b
ab
≤
a
+
b
2
1
x
1
x
x
+
1
x
2
≥
x
?
1
x
+
1
x
≥
2
x
?
1
x
x
+
1
x
≥
2
1
x
1
x
①
1
1
+
a
2
+
1
1
+
b
2
1
1
+
a
n
+
1
1
+
b
n
5
ax
ab
+
a
+
1
+
5
bx
bc
+
b
+
1
+
5
cx
ca
+
c
+
1
1
1
+
a
+
1
1
+
2
b
【考點】二元一次不定方程的應用.
【答案】1;1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:1030引用:4難度:0.2
相似題
-
1.為了節約用水,某市自來水收費規定是:如果每月用水不超過24噸,按每噸1.8元收費;如果超過24噸,超出的部分按每噸4元收費.已知某月,小張家比小王家多交了水費19元2角(用水按整數噸計算),問小張、小王兩家各交了多少水費?
發布:2024/6/27 10:35:59組卷:184引用:1難度:0.1 -
2.Let x(y+
)=2013,x and y are both positive integers,then the largest value of x+y is ,the smallest value of x+y is .1x
(英語小詞典:value值)發布:2024/7/6 8:0:9組卷:25引用:1難度:0.3 -
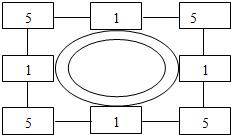 3.岳飛是我國古代宋朝的民族英雄,曾任通泰鎮撫史、兼泰州知州.據說在泰州抗擊金兵期間,有一次曾向將領們講了如下一個布陣圖,如圖4是一座城池,在城池的四周設了八個哨所,一共由24個衛士把守,按直線算,每邊都有11個人,后來由于軍情發生變化,連續四次給哨所增添兵力,每次增加4人,但要求在增加人員后,仍然保持每邊11個人把守.請問,兵力應如何調整?發布:2024/4/20 14:35:0組卷:281引用:6難度:0.5
3.岳飛是我國古代宋朝的民族英雄,曾任通泰鎮撫史、兼泰州知州.據說在泰州抗擊金兵期間,有一次曾向將領們講了如下一個布陣圖,如圖4是一座城池,在城池的四周設了八個哨所,一共由24個衛士把守,按直線算,每邊都有11個人,后來由于軍情發生變化,連續四次給哨所增添兵力,每次增加4人,但要求在增加人員后,仍然保持每邊11個人把守.請問,兵力應如何調整?發布:2024/4/20 14:35:0組卷:281引用:6難度:0.5


