當前位置：試卷中心 > 試卷詳情

2017-2018學年重慶一中八年級（下）開學數學試卷

發布：2024/4/20 14:35:0

一、選擇題

1．下列各數中，最小的實數是（　　）
A．1 B．0 C．-3 D．-1
組卷：51引用：5難度：0.9
解析
2．民族圖案是數學文化中的一塊瑰寶，下列圖案中既是軸對稱圖形也是中心對稱圖形的是（　　）
A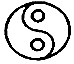． B． C． D．
組卷：88引用：8難度：0.8
解析
3．下列命題中，其中是真命題的是（　　）
A．同位角相等
B．x=1是方程x²=x的一個解
C．4的平方根是2
D．有兩邊及一角對應相等的兩個三角形全等
組卷：158引用：2難度：0.5
解析
4．在函數y=
x
+
1
x
-
2
中，自變量x的取值范圍是（　　）
A．x＞-1 B．x≥-1 C．x≥-1且x≠2 D．x＞-1且x≠2
組卷：771引用：11難度：0.7
解析
5．如圖，在△ABC中，DE∥BC，若AE=2，EC=3，則△ADE與△ABC的面積之比為（　　）
A．4：25 B．2：3 C．4：9 D．2：5
組卷：164引用：3難度：0.7
解析
6．估計2+
2
×
18
÷
3
的運算結果應在下列哪兩個整數之間（　　）
A．3和4 B．4和5 C．5和6 D．6和7
組卷：71引用：2難度：0.8
解析
7．按如圖所示的運算程序，能使輸出的結果為15的是（　　）
A．x=-2，y=3 B．x=2，y=-3 C．x=-8，y=3 D．x=8，y=-3
組卷：385引用：7難度：0.7
解析
8．如圖是用長度相等的火柴棒按一定規律構成的圖形，依此規律第9個圖形中火柴棒的根數是（　　）
A．46 B．47 C．55 D．57
組卷：344引用：5難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題

25．《見微知著》談到：從一個簡單的經典問題出發，從特殊到一般，由簡單到復雜：從部分到整體，由低維到高維，知識與方法上的類比是探索發展的重要途徑，是思想閥門發現新問題、新結論的重要方法．
閱讀材料一：
利用整體思想解題，運用代數式的恒等變形，使不少依照常規思路難以解決的問題找到簡便解決方法，常用的途徑有：（1）整體觀察；（2）整體設元；（3）整體代入；（4）整體求和等．
例如，ab=1求證：
1
1
+
a
+
1
1
+
b
=1
證明：原式=
ab
ab
+
a
+
1
1
+
b
=
b
1
+
b
+
1
1
+
b
=1
波利亞在《怎樣解題》中指出：“當你找到第一個藤菇或作出第一個發現后，再四處看看，他們總是成群生長”類似問題，我們有更多的式子滿足以上特征．
閱讀材料二：
基本不等式
ab
≤
a
+
b
2
（a＞0，b＞0），當且僅當a=b時等號成立，它是解決最值問題的有力工具．
例如：在x＞0的條件下，當x為何值時，x+
1
x
有最小值，最小值是多少？
解：∵x＞0，
1
x
＞0∴
x
+
1
x
2
≥
x
?
1
x
，即x
+
1
x
≥
2
x
?
1
x
，∴
x
+
1
x
≥
2

當且僅當x=
1
x
，即x=1時，x+
1
x
有最小值，最小值為2．
請根據閱讀材料解答下列問題：
（1）已知ab=1，求下列各式的值：
①
1
1
+
a
2
+
1
1
+
b
2
=
；
②
1
1
+
a
n
+
1
1
+
b
n
=
．
（2）若abc=1，解方程
5
ax
ab
+
a
+
1
+
5
bx
bc
+
b
+
1
+
5
cx
ca
+
c
+
1
=1
（3）若正數a、b滿足ab=1，求M=
1
1
+
a
+
1
1
+
2
b
的最小值．
組卷：1029引用：4難度：0.2
解析

五、解答題

26．如圖1，拋物線y=
3
6
x
2
+
4
3
3
x
+
2
3
與x軸交于點A，B（A在B左邊），與y軸交于點C，連AC，點D與點C關于拋物線的對稱軸對稱，過點D作DE∥AC交拋物線于點E，交y軸于點P．
（1）點F是直線AC下方拋物線上點一動點，連DF交AC于點G，連EG，當△EFG的面積的最大值時，直線DE上有一動點M，直線AC上有一動點N，滿足MN⊥AC，連GM，NO，求GM+MN+NO的最小值；
（2）如圖2，在（1）的條件下，過點F作FH⊥x軸于點H交AC于點L，將△AHL沿著射線AC平移到點A與點C重合，從而得到△A′H′L′（點A，H，L分別對應點A′，H′，L′），再將△A′H′L′繞點H′逆時針旋轉α（0°＜α＜180°），旋轉過程中，邊A′L′所在直線交直線DE于Q，交y軸于點R，求當△PQR為等腰三角形時，直接寫出PR的長．
組卷：646引用：5難度：0.1
解析