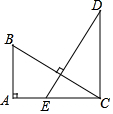
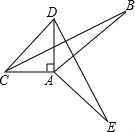
如圖,已知Rt△ABC,∠BAC=90°,在△ABC的外部分別以線段AB、AC、BC為邊作正方形ABDE、正方形ACFG、正方形BCPQ,連接AQ、DC,交點為M.
(1)判斷線段AQ、DC的關(guān)系,并說明理由;
(2)如圖①,過點A作AI⊥PQ,垂足為I,與邊BC交于點H,證明:S矩形BHIQ=S正方形ABDE;
(3)直接寫出S正方形ABDE,S正方形ACFG,S正方形BCPQ的數(shù)量關(guān)系;
(4)如圖②,在Rt△ABC中,若∠ABC=45°,AC=2,直接寫出線段AQ的長.

2
【答案】(1)DC=AQ,DC⊥AQ,證明見解析;
(2)見解析;
(3)S正方形ABDE+S正方形ACFG=S正方形BCPQ;
(4).
(2)見解析;
(3)S正方形ABDE+S正方形ACFG=S正方形BCPQ;
(4)
10
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/5 8:0:9組卷:41引用:1難度:0.5