問題提出
（1）如圖①，已知直線a∥b,點A，B在直線a上，點C，D在直線b上，則S△ACD==S△BCD（填“＞”“＜”或“=”）；
問題探究
（2）如圖②，⊙O的直徑為20，點A，B，C都在⊙O上，AB=12，求△ABC面積的最大值；
問題解決
（3）如圖③，在△ABC中，∠ACB=90°，AB=20，BC=10，根據(jù)設(shè)計要求，點D為∠ABC內(nèi)部一點，且∠ADB=60°，過點C作CE∥AD交BD于點E，連接AE，CD，試求滿足設(shè)計要求的四邊形ADCE的最大面積．
【考點】圓的綜合題．
【答案】=
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：876引用：5難度：0.4
相似題
-
1．在平面直角坐標系xOy中，對于點C和圓P，給出如下定義：
若圓P上存在A、B兩點，使得△ABC是等腰直角三角形，且∠ABC=90°，則稱點C是圓P的“等垂點”．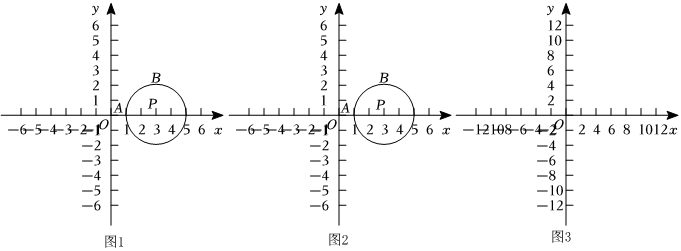
（1）當點P坐標為（3，0），且圓P的半徑為2時．
①如圖1，若圓P上存在兩點A（1，0）和B（3，2），請直接寫出此時圓P的“等垂點”C的坐標 ；
②如圖2，若直線y=x+b上存在圓P的“等垂點”，求b的取值范圍；
（2）設(shè)圓P的圓心P在y軸上，半徑為2．
若直線y=-x上存在點R，使半徑為1的圓R上有點S是圓P的“等垂點”，請直接寫出圓心P的縱坐標的取值范圍．發(fā)布：2025/6/9 12:30:2組卷：127引用：3難度：0.4 -
2．綜合與實踐
問題情境：如圖，將一個圓錐的側(cè)面展開后可得到一個圓心角為n°，半徑為l的扇形BOB′，圓錐底面是一個半徑為r的圓．母線OA在展開圖上對應(yīng)的半徑OA′經(jīng)過的中點．?BB′
特例研究：（1）當r=3，l=9時，n= ，展開圖上，OA′與OB的夾角為 °．
問題提出：（2）求證：n=．360rl
問題解決：（3）如圖2，一種紙質(zhì)圓錐形生日帽，底面直徑為12cm,母線長也為12cm,為了美觀，想在底面圓上一點A和與之相對的母線PB中點C之間拉一條細彩帶進行裝飾，求彩帶長度的最小值．（提示：嘗試畫出圓錐側(cè)面展開圖）發(fā)布：2025/6/9 7:30:1組卷：130引用：2難度：0.4 -
3．定義：對角線互相垂直的圓內(nèi)接四邊形稱為圓的神奇四邊形．
（1）如圖1，已知四邊形ABCD是⊙O的神奇四邊形，若AC=12，BD=10，則S四邊形ABCD=；
（2）如圖2，已知四邊形ABCD為⊙O的內(nèi)接四邊形，連接OA，OB，OC，OD，滿足∠BOC+∠AOD=180°，求證：四邊形ABCD是⊙O的神奇四邊形；
（3）如圖3，已知四邊形ABCD是⊙O的神奇四邊形，∠BAD=90°，延長AD，BC相交于點E，若AB=6，AE=8，求AC的長．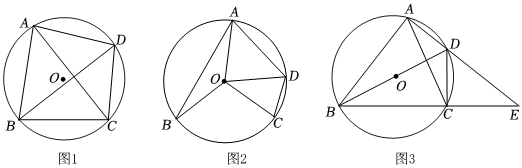
發(fā)布：2025/6/9 7:0:1組卷：213引用：1難度：0.6