（1）問(wèn)題背景：
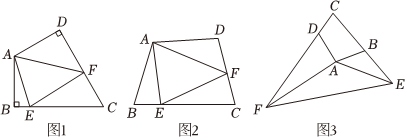
如圖1，在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F(xiàn)分別是BC、CD上的點(diǎn)，且∠EAF=60°．探究圖中線(xiàn)段BE，EF，F(xiàn)D之間的數(shù)量關(guān)系．
小明同學(xué)探究此問(wèn)題的方法是，延長(zhǎng)FD到點(diǎn)G，使DG=BE，連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結(jié)論，他的結(jié)論應(yīng)是 BE+FD=EFBE+FD=EF；
（2）靈活運(yùn)用：
如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°．E，F(xiàn)分別是BC，CD上的點(diǎn)，且∠EAF=12∠BAD，上述結(jié)論是否仍然成立，請(qǐng)說(shuō)明理由；
（3）探索延伸：
如圖3，已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD，若點(diǎn)E在CB的延長(zhǎng)線(xiàn)上，點(diǎn)F在CD的延長(zhǎng)線(xiàn)上，如圖3所示，且滿(mǎn)足EF=BE+FD，請(qǐng)直接寫(xiě)出∠EAF與∠DAB的數(shù)量關(guān)系．
1
2
【考點(diǎn)】四邊形綜合題．
【答案】BE+FD=EF
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/31 16:0:9組卷：298引用：2難度：0.5
相似題
-
1．已知：△ABC中，AB=AC，∠BAC=α，P是邊BC上一點(diǎn)，逆時(shí)針把AP旋轉(zhuǎn)α角到AE（即AE=AP，∠PAE=∠BAC=α），作ED∥BC交直線(xiàn)AB于D．
（1）求證：四邊形PCDE是平行四邊形；
（2）若α=120°，AB=3．
①當(dāng)四邊形PCDE為菱形，試在圖2中畫(huà)出圖形，并求出CP的值；
②當(dāng)四邊形PCDE為矩形，如圖3，直接寫(xiě)出矩形PCDE面積的值 ．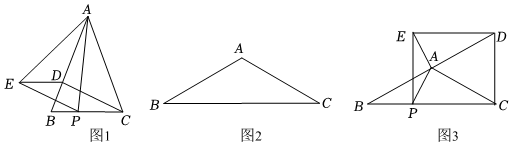
發(fā)布：2025/6/15 9:30:1組卷：30引用：1難度：0.3 -
2．（1）如圖1，點(diǎn)P是?ABCD內(nèi)的一點(diǎn)，分別過(guò)點(diǎn)B、C、D作AP的垂線(xiàn)BE、CF、DH，垂足分別為E、F、H，猜想BE、CF、DH三者之間的關(guān)系，并證明；
（2）如圖2，若點(diǎn)P在?ABCD的外部，△APB的面積為18，△APD的面積為3，求△APC的面積；
（3）如圖3，在（2）條件下，AB=BC，∠APC=∠ABC=90°，設(shè)AP、BP分別于CD相交于點(diǎn)M、N，=（請(qǐng)直接寫(xiě)出結(jié)論）．CPPM
發(fā)布：2025/6/15 11:0:2組卷：51引用：2難度：0.3 -
3．已知矩形ABCD，把△BCD沿BD翻折，得△BDG，BG，AD所在的直線(xiàn)交于點(diǎn)E，過(guò)點(diǎn)D作DF∥BE交BC所在直線(xiàn)于點(diǎn)F．
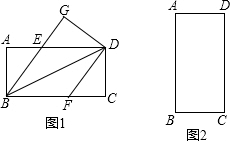
（1）如圖1，AB＜AD，
①求證：四邊形BEDF是菱形；
②若AB=4，AD=8，求四邊形BEDF的面積；
（2）如圖2，若AB=8，AD=4，請(qǐng)按要求畫(huà)出圖形，并直接寫(xiě)出四邊形BEDF的面積．發(fā)布：2025/6/15 10:30:2組卷：163引用：2難度：0.3