已知點P是矩形ABCD邊AB上的任意一點（與點A、B不重合）．
（1）如圖①，現將△PBC沿PC翻折得到△PEC；再在AD上取一點F，將△PAF沿PF翻折得到△PGF，并使得射線PE、PG重合，試問FG與CE的位置關系如何，請說明理由；
（2）在（1）中，如圖②，連接FC，取FC的中點H，連接GH、EH，請你探索線段GH和線段EH的大小關系，并說明你的理由；
（3）如圖③，分別在AD、BC上取點F、C′，使得∠APF=∠BPC′，與（1）中的操作相類似，即將△PAF沿PF翻折得到△PFG，并將△PBC′沿PC′翻折得到△PEC′，連接FC′，取FC′的中點H，連接GH、EH，試問（2）中的結論還成立嗎？請說明理由．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1312引用：21難度：0.1
相似題
-
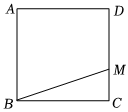1．如圖，正方形ABCD的邊長為4，點M為DC邊上一動點，將△BCM沿直線BM翻折，使得點C落在同一平面內的點C'處，連接DC'并延長交正方形ABCD一邊于點N．當BN=DM時，CM的長為（ ）發布：2025/5/22 14:30:2組卷：202引用：4難度：0.7 -
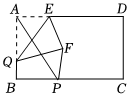2．如圖，矩形ABCD中，AB=2，點E在AD上，AE=1．P、Q分別是BC、AB上的兩個動點，△AEQ沿EQ翻折形成△FEQ，連接PF、PA，則PF+PA的最小值是 ．發布：2025/5/22 14:30:2組卷：283引用：5難度：0.5 -
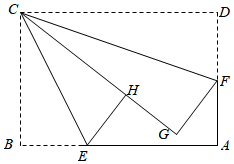3．如圖，在矩形紙片ABCD中，點E、F分別在矩形的邊AB、AD上，將矩形紙片沿CE、CF折疊，點B落在H處，點D落在G處，點C、H、G恰好在同一直線上，若AB=6，AD=4，BE=2，則DF的長是（ ）發布：2025/5/22 14:30:2組卷：2377引用：7難度：0.6