“半角型”問題探究：
（1）如圖1，在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，且∠EAF=60°，探究圖中線段BE，EF，FD之間的數量關系．
小明同學的方法是將△ABE繞點A逆時針旋轉120°到△ADG的位置，然后再證明△AFE≌△AFG，從而得出結論：EF=BE+DFEF=BE+DF
（2）如圖2，在四邊形ABCD中，AB=AD，∠B+∠D=180°，E，F分別是邊BC，CD上的點，且∠EAF=12∠BAD，上述結論是否仍然成立，并說明理由．
歸納應用
（3）正方形ABCD中，點E、F分別在BC、CD上，且∠EAF=45°，已知BE=3，DF=2，求正方形ABCD的邊長．
拓展提高
（4）邊長為4的正方形ABCD中，點E、F分別在AB、CD上，AE=CF=1，O為EF的中點，動點G、H分別在邊AD、BC上，EF與GH的交點P在O、F之間（與O、F不重合），且∠GPE=45°，設AG=m,求m的取值范圍．
1
2
【考點】四邊形綜合題．
【答案】EF=BE+DF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：2604引用：4難度：0.3
相似題
-
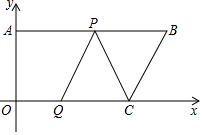1．如圖，在平面直角坐標系中，AB∥OC，A（0，12），B（a,c），C（b,0），并且a,b滿足b=+a-20+16．動點P從點A出發，在線段AB上以每秒2個單位長度的速度向點B運動；動點Q從點O出發，在線段OC上以每秒1個單位長度的速度向點C運動，點P，Q分別從點A，O同時出發，當點P運動到點B時，點Q隨之停止運動．設運動時間為t秒．20-a
（1）直接寫出B，C兩點的坐標；
（2）當t為何值時，四邊形PQCB是平行四邊形？
（3）當t為何值時，△PQC是以PQ為腰的等腰三角形？并求出P，Q兩點的坐標．發布：2025/6/5 10:0:2組卷：450引用：5難度：0.2 -
2．如圖，在邊長為4的正方形ABCD中，點P在AB上從A向B運動，連接DP交AC于點Q．
（1）試證明：無論點P運動到AB上何處時，都有△ADQ≌△ABQ；
（2）當△ABQ的面積是正方形ABCD面積的時，求DQ的長；16
（3）若點P從點A運動到點B，再繼續在BC上運動到點C，在整個運動過程中，當點P運動到什么位置時，△ADQ恰為等腰三角形．發布：2025/6/5 10:0:2組卷：268引用：11難度：0.3 -
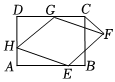3．已知，如圖，矩形ABCD中，AD=6，DC=8，菱形EFGH的三個頂點E，G，H分別在矩形ABCD的邊AB，CD，DA上，AH=2，連接CF．
（1）若DC=2，求證：四邊形EFGH為正方形；
（2）當點G在邊CD上運動時，點F到直線CD的距離是否為定值？若是，請求出這個定值；若不是，請說明理由．
（3）試說明當點C運動到何處時，△FCG的面積最小，并求出這個最小值．
?發布：2025/6/5 9:30:2組卷：25引用：1難度：0.2