已知矩形ABCD和點(diǎn)P，當(dāng)點(diǎn)P在BC上任一位置（如圖（1）所示）時，易證得結(jié)論：PA2+PC2=PB2+PD2，請你探究：當(dāng)點(diǎn)P分別在圖（2）、圖（3）中的位置時，PA2、PB2、PC2和PD2又有怎樣的數(shù)量關(guān)系請你寫出對上述兩種情況的探究結(jié)論，并利用圖（2）證明你的結(jié)論．
答：對圖（2）的探究結(jié)論為PA2+PC2=PB2+PD2PA2+PC2=PB2+PD2；
對圖（3）的探究結(jié)論為PA2+PC2=PB2+PD2PA2+PC2=PB2+PD2；
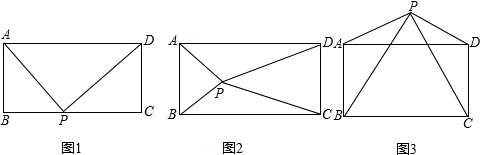
證明：如圖（2）
【考點(diǎn)】矩形的判定與性質(zhì)．
【答案】PA2+PC2=PB2+PD2；PA2+PC2=PB2+PD2
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：7096引用：32難度：0.1
相似題
-
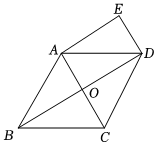1．如圖，在菱形ABCD中，對角線AC，BD相交于點(diǎn)O．過點(diǎn)A作AE∥BD，過點(diǎn)D作DE∥AC交AE于點(diǎn)E．
（1）求證：四邊形AODE是矩形；
（2）若AB=2，∠ABC=60°，求四邊形AODE的面積．發(fā)布：2025/6/4 17:30:2組卷：1434引用：13難度：0.5 -
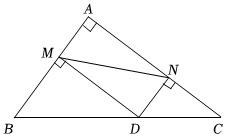2．如圖，在Rt△ABC中，∠BAC=90°，且BA=6，AC=8，點(diǎn)D是斜邊BC上的一個動點(diǎn)，過點(diǎn)D分別作DM⊥AB于點(diǎn)M，DN⊥AC于點(diǎn)N，連接MN，則線段MN的最小值為（ ）發(fā)布：2025/6/4 19:30:1組卷：969引用：4難度：0.5 -
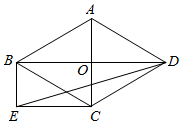3．如圖，菱形ABCD的對角線AC，BD相交于點(diǎn)O，過B點(diǎn)作BE∥AC，且BE=AC，連結(jié)EC，ED．12
（1）求證：四邊形BECO是矩形；
（2）若AC=2，∠ABC=60°，求DE的長．發(fā)布：2025/6/4 21:30:2組卷：731引用：6難度：0.7