我國的紙傘工藝十分巧妙．如圖①，傘不論張開還是縮攏，傘柄AP始終平分同一平面內兩條傘骨所成的角∠BAD，從而保證傘圈C能沿著傘柄滑動．小明受此啟發設計了一個“簡易平分角儀器”，如圖②，其中AB=AD，BC=DC，將儀器上的點A與∠PRQ的頂點R重合，調整AB和AD，使它們落在角的兩邊上，沿AC畫一條射線AE，則AE為∠PRQ的平分線．
（1）如圖②，試說明這個平分角的儀器的制作原理；
（2）如圖③，將上述平分角儀器的頂點A落在⊙O的直徑MN的端點M處，邊AB與直徑MN共線，邊AD與⊙O相交于點G，AC交⊙O于點E，過點E作⊙O的切線，與AD，BC分別交于點F，H．
①求證：EF⊥AD；
②若⊙O半徑為3，AE=4，求EF的長．
【考點】圓的綜合題．
【答案】（1）見解答；
（2）①見解答；
②．
（2）①見解答；
②
4
5
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/30 8:0:9組卷：70引用：1難度：0.5
相似題
-
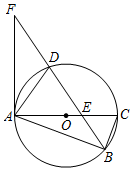1．如圖，⊙O是Rt△ABC的外接圓，∠ABC=90°，D為圓上一點，且B，D兩點位于AC異側，連接BD，交AC于E，點F為BD延長線上一點，連接AF，使得∠DAF=∠ABD．
（1）求證：AF為⊙O的切線；
（2）當點D為EF的中點時，求證：AD2=AO?AE；
（3）在（2）的條件下，若sin∠BAC=，AF=213，求BF的長．6發布：2025/5/24 18:0:1組卷：2315引用：10難度：0.1 -
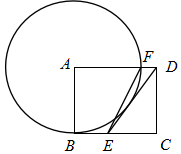2．如圖，在矩形ABCD中，點E是BC邊上一點，且AD=DE，以AB為半徑作⊙A，交AD邊于點F，連接EF．
（1）求證：DE是⊙A的切線；
（2）若AB=2，BE=1，求AD的長；
（3）在（2）的條件下，求tan∠FED．發布：2025/5/24 17:30:1組卷：161引用：2難度：0.4 -
3．（1）如圖1，⊙A的半徑為2，AB=5，點P為⊙A上任意一點，則BP的最小值為 ．
（2）如圖2，已知矩形ABCD，點E為AB上方一點，連接AE，BE，作EF⊥AB于點F，點P是△BEF的內心，求∠BPE的度數．
（3）如圖3，在（2）的條件下，連接AP，CP，若矩形的邊長AB=6，BC=4，BE=BA，求此時CP的最小值．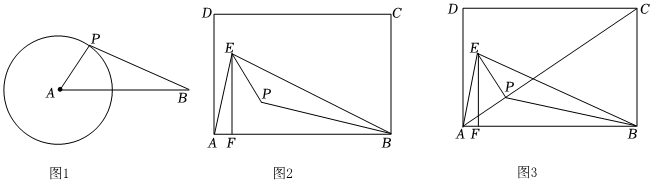
發布：2025/5/24 16:30:1組卷：1241引用：6難度：0.3