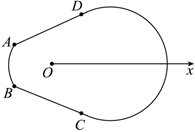
有一種燈泡截面類似“梨形”曲線，如圖所示，它是由圓弧?AB、圓弧?CD和線段AD、BC四部分組成，在平面直角坐標系xOy中，以坐標原點O為極點，x軸正半軸為極軸，建立極坐標系．已知A（2，5π6），B（2，7π6），C（3，-π3），D（3，π3），弧?AB、弧?CD所在圓的圓心分別是（0，0）、（3，0），曲線M1是弧?AB，曲線M2是弧?CD．
（1）分別寫出M1，M2的極坐標方程；
（2）直線l的參數方程為x=6+t y=63-at
（t為參數），若l與曲線M2有且僅有兩個公共點，求a的取值范圍．
?
AB
?
CD
A
（
2
，
5
π
6
）
，
B
（
2
，
7
π
6
）
，
C
（
3
，-
π
3
）
，
D
（
3
，
π
3
）
?
AB
?
CD
?
AB
?
CD
x = 6 + t |
y = 6 3 - at |
【考點】參數方程化成普通方程．
【答案】（1）；；
（2）．
M
1
：
ρ
=
2
，
θ
∈
[
5
π
6
，
7
π
6
]
M
2
：
ρ
=
6
cosθ
，
θ
∈
[
-
π
3
，
π
3
]
（2）
（
-
∞
，-
5
3
3
]
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：85引用：2難度：0.5
相似題
-
1．在平面直角坐標系xOy中，已知曲線C1：
（t為參數），以坐標原點O為極點，x軸正半軸為極軸建立極坐標系，曲線C2：ρ=2acosθ（a＞0）．x=t,y=2t2-t+32
（1）求曲線C1的極坐標方程和曲線C2的直角坐標方程；
（2）設射線與C1相交于A，B兩點，與C2相交于M點（異于O），若|OM|=|AB|，求a.θ=π3（ρ≥0）發布：2024/12/29 6:30:1組卷：154引用：8難度：0.7 -
2．已知三個方程：①
②x=ty=t2③x=tanty=tan2t（都是以t為參數）．那么表示同一曲線的方程是（ ）x=sinty=sin2t發布：2025/1/7 22:30:4組卷：105引用：2難度：0.7 -
3．直線l：
（t為參數，a≠0），圓C：x=a-2t,y=-1+t（極軸與x軸的非負半軸重合，且單位長度相同）．ρ=22cos（θ+π4）
（1）求圓心C到直線l的距離；
（2）若直線l被圓C截得的弦長為，求a的值．655發布：2024/12/29 10:0:1組卷：56引用：6難度：0.5