2022-2023學(xué)年重慶市萬(wàn)州中學(xué)教育集團(tuán)九年級(jí)（下）期中數(shù)學(xué)試卷

一．選擇題（每題4分，本大題共10個(gè)小題，共40分）

• 1．在代數(shù)式

  2

  xy

  x

  ，2x+y,

  2

  xy

  3

  ，

  a

  2

  -

  b

  π

  ，

  2

  a

  +

  b

  ，

  2

  x

  -

  1

  中，是分式的有（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：207引用：1難度：0.8

  解析

• 2．芯片是手機(jī)、電腦等高科技產(chǎn)品的核心部件，目前我國(guó)芯片已可采用14納米工藝．已知14納米為0.000000014米，數(shù)據(jù)0.000000014用科學(xué)記數(shù)法表示為（　　）

  A．1.4×10-10

  B．1.4×10-8

  C．14×10-8

  D．1.4×10-9
  組卷：1271引用：20難度：0.9

  解析

• 3．在函數(shù)

  y

  =

  |

  x

  |

  -

  1

  x

  -

  2

  中，自變量x的取值范圍是（　　）

  A．x≥1

  B．x≠2

  C．x≥1且x≠2

  D．x≠1且x≠2
  組卷：411引用：2難度：0.8

  解析

• 4．把分式

  2

  x

  +

  3

  y

  x

  2

  -

  y

  2

  的x、y均縮小為原來(lái)的10倍后，則分式的值（　　）

  A．為原分式值的 1 10	B．為原分式值的 1 100
  C．為原分式值的10倍	D．不變
  組卷：339引用：1難度：0.8

  解析

• 5．下列四個(gè)選項(xiàng)中，不符合直線y=-x-3的性質(zhì)特征的選項(xiàng)是（　　）

  A．經(jīng)過(guò)第二、三、四象限	B．y隨x的增大而減小
  C．與x軸交于（3，0）	D．與y軸交于（0，-3）
  組卷：626引用：6難度：0.7

  解析

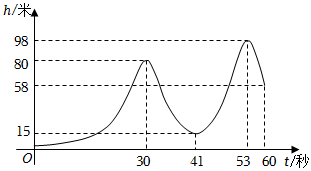• 6．4月春游季，小紅和小伙伴在草坪上放風(fēng)箏，記錄了在某一段60秒時(shí)間內(nèi)風(fēng)箏的高度h（米）與時(shí)間t（秒）之間的函數(shù)關(guān)系圖象如圖所示，下列結(jié)論錯(cuò)誤的是（　　）

  A．風(fēng)箏距水平地面的最高高度為98米

  B．當(dāng)t=41時(shí)，h=15

  C．當(dāng)30＜t≤41時(shí)，高度h（米）隨時(shí)間t（秒）的增大而減小

  D．在0≤t≤60范圍內(nèi)，當(dāng)風(fēng)箏高度是80米時(shí)，t的值只能等于30
  組卷：202引用：1難度：0.8

  解析

• 7．如圖，《四元玉鑒》是我國(guó)古代數(shù)學(xué)重要著作之一，為元代數(shù)學(xué)家朱世杰所著．該著作記載了“買椽多少”問(wèn)題：“六貫二百一十錢(qián)，倩人去買幾株椽．每株腳錢(qián)三文足，無(wú)錢(qián)準(zhǔn)與一株椽”．大意是：現(xiàn)請(qǐng)人代買一批椽，這批椽的價(jià)錢(qián)為6210文．如果每株椽的運(yùn)費(fèi)是3文，那么少拿一株椽后，剩下的椽的運(yùn)費(fèi)恰好等于一株椽的價(jià)錢(qián)，試問(wèn)6210文能買多少株椽？（椽，裝于屋頂以支持屋頂蓋材料的木桿）設(shè)這批椽有x株，則符合題意的方程是（　　）

  A． 6210 x = 3	B． 6210 x = 3 x - 1
  C． 3 （ x - 1 ） = 6210 x	D． 3 （ x - 1 ） = 6210 x - 1
  組卷：309引用：4難度：0.6

  解析

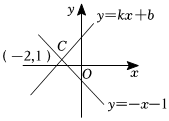• 8．如圖，直線y=-x-1與y=kx+b（k≠0且k,b為常數(shù)）的交點(diǎn)坐標(biāo)為（-2，1）．則關(guān)于x的不等式-x-1＜kx+b的解集為（　　）

  A．x＞-2

  B．x＜-2

  C．x＞1

  D．x＜1
  組卷：823引用：1難度：0.7

  解析

四．解答題（本大題共6個(gè)小題，第21-25小題每小題10分，第26題12分，共62分）

• 25．如圖1，直線

  l

  1

  ：

  y

  =

  -

  1

  4

  x

  +

  1

  與x軸，y軸分別交于A，B兩點(diǎn)，直線l₂與x軸，y軸分別交于C，D兩點(diǎn)，兩直線相交于點(diǎn)P，已知點(diǎn)C的坐標(biāo)為（-2，0），點(diǎn)P的橫坐標(biāo)為

  -

  4

  5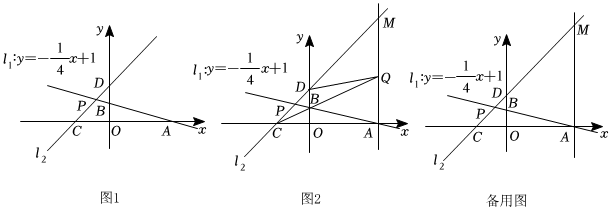

  ．
  
  （1）直接寫(xiě)出點(diǎn)A、P的坐標(biāo)，并求出直線l₂的函數(shù)表達(dá)式；
  （2）如圖2，過(guò)點(diǎn)A作x軸的垂線，交直線l₂于點(diǎn)M，點(diǎn)Q是線段AM上的一動(dòng)點(diǎn)，連接QD，QC，當(dāng)△QDC的周長(zhǎng)最小時(shí)，求點(diǎn)Q的坐標(biāo)和周長(zhǎng)的最小值．
  （3）在第（2）問(wèn)的條件下，若點(diǎn)N是直線AM上的一個(gè)動(dòng)點(diǎn)，以D，Q，N三點(diǎn)為頂點(diǎn)的三角形是等腰三角形，請(qǐng)直接寫(xiě)出此時(shí)點(diǎn)N的坐標(biāo)．
  組卷：492引用：3難度：0.3

  解析

• 26．在△ABC中，∠BAC=90°，

  AB

  =

  AC

  =

  2

  2

  ，D為BC上任意一點(diǎn)，E為AC上任意一點(diǎn)．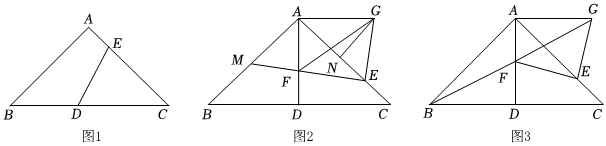
  
  （1）如圖1，連接DE，若∠CDE=60°，AC=4AE，求DE的長(zhǎng)．
  （2）如圖2，若點(diǎn)D為BC中點(diǎn)，連接AD，點(diǎn)F為AD上任意一點(diǎn)，連接EF并延長(zhǎng)交AB于點(diǎn)M，將線段EF繞點(diǎn)E順時(shí)針旋轉(zhuǎn)90°得到線段EG，連接AG．點(diǎn)N在AC上，∠AGN=∠AEG且

  AM

  +

  AF

  =

  2

  AE

  ，求證：GN=MF．
  （3）如圖3，點(diǎn)D為BC中點(diǎn)，連接AD，點(diǎn)F為AD的中點(diǎn)，連接EF、BF，將線段EF繞點(diǎn)E順時(shí)針旋轉(zhuǎn)90°得到線段EG，連接AG，H為直線AB上一動(dòng)點(diǎn)，連接FH，將△BFH沿FH翻折至△ABC所在平面內(nèi)，得到△B′FH，連接B′G，直接寫(xiě)出線段B′G的長(zhǎng)度的最大值．
  組卷：415引用：2難度：0.1

  解析