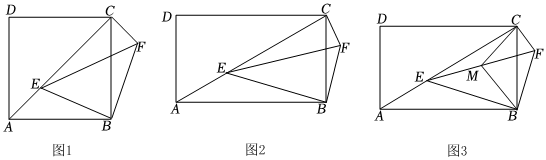
（1）已知正方形ABCD，E為對角線AC上一動點，將BE繞點B順時針旋轉90°到BF處，得△BEF，連接CF，如圖1，填空：
①CFAE=11；
②∠ACF的度數為 90°90°．
（2）在矩形ABCD和Rt△BEF中，∠EBF=90°，∠ACB=∠EFB=60°，連接CF，如圖2，請判斷CFAE的值及∠ACF的度數，并說明理由．
（3）在（2）的條件下，取EF的中點M，連接BM、CM，若AB=23，則當△CBM是直角三角形時，請直接寫出線段CF的長．
CF
AE
CF
AE
3
【考點】四邊形綜合題．
【答案】1；90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：327引用：3難度：0.4
相似題
-
1．如圖，四邊形ABCD中，∠A=∠B=90°，AD=2，AB=5，BC=3．
（1）如圖①，P為AB上的一個動點，以PD，PC為邊作?PCQD．
①請問四邊形PCQD能否成為矩形？若能，求出AP的長；若不能，請說明理由．
②填空：當AP=時，四邊形PCQD為菱形；
③填空：當AP=時，四邊形PCQD有四條對稱軸．
（2）如圖②，若P為AB上的一點，以PD，PC為邊作?PCQD，請問對角線PQ的長是否存在最小值？若存在，請求出最小值；若不存在，請說明理由．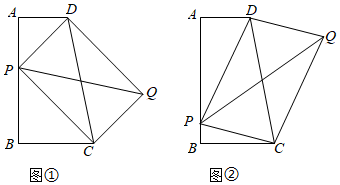
發布：2025/5/24 11:0:1組卷：701引用：3難度：0.2 -
2．綜合與實踐
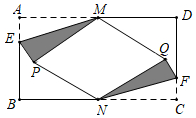
問題情境：在數學活動課上，老師讓同學們以“矩形的折疊”為主題開展數學活動如圖，矩形紙片ABCD中，點M、N分別是AD、BC的中點，點E、F分別在AB、CD上，且AE=CF．
動手操作：將△AEM沿EM折疊，點A的對應點為點P，將△NCF沿NF折疊，點C的對應點為點Q，點P、Q均落在矩形ABCD的內部，連接PN、QM．
問題解決：（1）判斷四邊形PNQM的形狀，并證明；
（2）當AD=2AB=4，四邊形PNQM為菱形時，求AE的長．發布：2025/5/24 11:30:1組卷：112引用：2難度：0.3 -
3．在四邊形ABCD中，AB=BC，∠B=60°；
（1）如圖1，已知，∠D=30°求得∠A+∠C的大小為．
（2）已知AD=3，CD=4，在（1）的條件下，利用圖1，連接BD，并求出BD的長度；
（3）問題解決；如圖2，已知∠D=75°，BD=6，現需要截取某種四邊形的材料板，這個材料板的形狀恰巧符合如圖2所示的四邊形，為了盡可能節約，你能求出這種四邊形面積的最小值嗎？如果能，請求出此時四邊形ABCD面積的最小值；如果不能，請說明理由．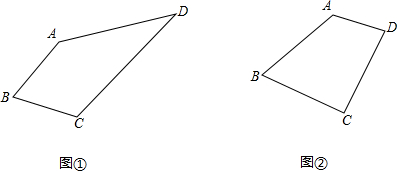
發布：2025/5/24 12:0:1組卷：527引用：3難度：0.1