學(xué)完勾股定理的證明后發(fā)現(xiàn)運(yùn)用“同一圖形的面積不同表示方式相同”可以證明一類含有線段的等式，這種解決問題的方法我們稱之為等面積法．
（1）【學(xué)有所用】如圖1，在等腰△ABC中，AB=AC，其一腰上的高BD為h,M是底邊BC上的任意一點，M到腰AB、AC的距離ME、MF分別為h1、h2，小明發(fā)現(xiàn)，通過連接AM，將△ABC的面積轉(zhuǎn)化為△ABM和△ACM的面積之和，建立等量關(guān)系，便可證明h1+h2=h,請你結(jié)合圖形來證明：h1+h2=h；
（2）【嘗試提升】如圖2，在△ABC中，∠A=90°，D是AB邊上一點，使BD=CD，過BC上一點P，作PE⊥AB，垂足為點E，作PF⊥CD，垂足為點F，已知AB=62，BC=63，求PE+PF的長．
（3）【拓展遷移】如圖3，在平面直角坐標(biāo)系中有兩條直線l1：y=-512x-5，l2：y=5x-5，若l2上的一點M到l1的距離是2，求BMCM的值．
2
3
5
12
BM
CM
【考點】一次函數(shù)綜合題．
【答案】（1）證明見解答；
（2）6；
（3）=或．
（2）6；
（3）
BM
CM
2
3
2
7
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/10/4 9:0:2組卷：877引用：4難度：0.4
相似題
-
1．已知直線y=-
x+3與x軸，y軸分別交于A，B兩點，在坐標(biāo)軸上取一點P，使得△PAB是等腰三角形，則符合條件的點P有（ ）個3發(fā)布：2025/5/28 2:30:1組卷：1279引用：2難度：0.5 -
2．已知：在坐標(biāo)平面內(nèi)A（0，0）、B（12，0）、C（12，6）、D（0，6），點Q、P分別沿DA、AB從D、A向A、B以1單
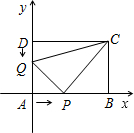位/秒，2單位/秒的速度移動，同時出發(fā)，t表示移動時間（0≤t≤6）．
（1）寫出△PQA的面積S與t的函數(shù)關(guān)系式．
（2）四邊形APCQ的面積與t有關(guān)嗎？說明理由．
（3）t等于多少時，△APQ為軸對稱圖形．
（4）PQ能否與AC垂直？若能，求出直線PQ的解析式；若不能，說明理由．發(fā)布：2025/5/28 5:0:1組卷：562引用：2難度：0.1 -
3．在直角坐標(biāo)系中，O為原點，A在y軸上，C在x軸上，矩形OABC的頂點B的坐標(biāo)為（15，6），直線
恰好將矩形OABC分成面積相等的兩部分，那么b=．y=12x+b發(fā)布：2025/5/28 5:30:2組卷：225引用：1難度：0.5