已知直線y=kx-2k+3(k≠0)與拋物線y=12(x-2)2相交于A、B兩點(點A在點B的左側).
(1)不論k取何值,直線y=kx-2k+3必經(jīng)過定點P,直接寫出點P的坐標;
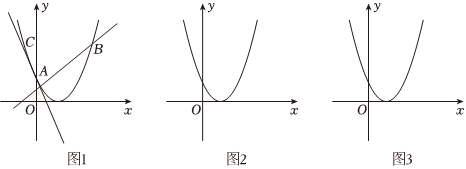
(2)如圖,已知B、C兩點關于拋物線y=12(x-2)2的對稱軸對稱.
①求證:直線AC必經(jīng)過一定點;
②當m≤x≤m+1時,y的最大值與最小值的差為2,求m的值.
y
=
1
2
(
x
-
2
)
2
y
=
1
2
(
x
-
2
)
2
【考點】二次函數(shù)的性質;二次函數(shù)的最值;二次函數(shù)圖象上點的坐標特征;一次函數(shù)圖象與系數(shù)的關系;一次函數(shù)圖象上點的坐標特征;坐標與圖形變化-對稱.
【答案】(1)點P的坐標為(2,3);
(2)①過定點(2,-3);②m的值為-或.
(2)①過定點(2,-3);②m的值為-
1
2
7
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/9/17 1:0:8組卷:152引用:1難度:0.5
相似題
-
1.已知函數(shù)y=k2x2+k(2x-3x2)+2x2-2x+1的圖象不經(jīng)過第四象限,求常數(shù)k的取值范圍.
發(fā)布:2025/5/28 4:30:1組卷:202引用:2難度:0.5 -
2.已知函數(shù)y=-
x2+12在0<a≤x≤b時,有2a≤y≤2b,則(a,b)=132.發(fā)布:2025/5/28 6:30:1組卷:156引用:2難度:0.7 -
3.若拋物線y=-x2+2ax+b的頂點在直線mx-y-2m+1=0上移動,且與拋物線y=x2有公共點,求m的取值范圍.
發(fā)布:2025/5/28 4:30:1組卷:654引用:1難度:0.5


