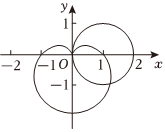
如圖，在平面直角坐標系xOy中，以坐標原點為極點，極軸所在的直線為x軸建立極坐標系，曲線C₁是經過極點且圓心在極軸上的直徑為2的圓，曲線C₂是著名的笛卡爾心形曲線，它的極坐標方程為ρ=1-sinθ（θ∈[0，2π]）．
（1）求曲線C₁的極坐標方程，并求曲線C₁和曲線C₂的交點（異于極點）的極徑；
（2）若曲線C₃的參數方程為
x
=
tcos
π
6
y
=
tsin
π
6
（t為參數），且曲線C₃和曲線C₂相交于除極點以外的M，N兩點，求線段MN的長度．

【答案】（1）

；（2）2．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/7/31 8:0:9組卷：18引用：1難度：0.5

相似題

1．在直角坐標系xOy中，以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C₁：ρcosθ=3，曲線C₂：ρ=4cosθ（
0
≤
θ
＜
π
2
）．
（1）求C₁與C₂交點的極坐標；
（2）設點Q在C₂上，
OQ
=
2
3
QP
，求動點P的極坐標方程．
發布：2024/12/29 3:0:1組卷：144引用：5難度：0.3
解析
2．極坐標方程ρcosθ=2sin2θ表示的曲線為（　　）
A．一條射線和一個圓 B．一條直線和一個圓
C．兩條直線 D．一個圓
發布：2024/12/29 2:30:1組卷：244引用：6難度：0.7
解析
3．已知點的極坐標是
（
3
，
π
4
）
，則它的直角坐標是

．
發布：2024/12/29 12:30:1組卷：12引用：2難度：0.7
解析

相關試卷

A．一條射線和一個圓	B．一條直線和一個圓
C．兩條直線	D．一個圓

1．在直角坐標系xOy中，以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C1：ρcosθ=3，曲線C2：ρ=4cosθ（0≤θ＜π2）．（1）求C1與C2交點的極坐標；（2）設點Q在C2上，OQ=23QP，求動點P的極坐標方程．