如圖1，△ABC，△EDC是兩個等腰直角三角形，其中∠ABC=∠EDC=90°，AB=5，DE=3，連接AE，取AE中點F，連接BF，DF．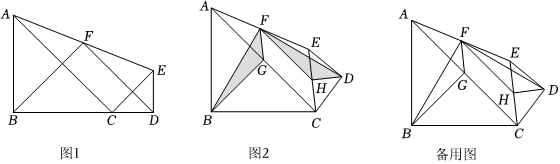
（1）如圖1，當B，C，D三個點共線時，請直接寫出BF與DF的數量關系與位置關系；
（2）如圖2，將△EDC繞點C逆時針旋轉，取AC與EC的中點G，H，當點G，H，F三點不共線時，連接GF，HF，BG，DH，求證：△BGF≌△FHD；
（3）在（2）的條件下，連接BD，在△EDC繞點C旋轉的過程中，求△BFD面積的最小值，并說明理由．

【答案】（1）BF=DF，BF⊥DF；
（2）證明見解析；
（3）1，理由見解析．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/8/5 8:0:8組卷：416引用：3難度：0.2

相似題

1．在綜合與實踐課上，劉老師展示了一個情境，讓同學們進行探究：情境呈現：如圖1，等腰直角三角形ABC中，AC=BC，∠ACB=90°，點P為AC上一點，過點P作PQ⊥AB，垂足為Q，連接BP，點D為BP的中點，連接CD，DQ．

分別過點Q，C作QM⊥AB，CN⊥AB，垂足分別為M，N．
∵△ABC和△AQP都是等腰直角三角形，QM⊥AP，CN⊥AB，
∴
QM
=
AM
=
PM
=
1
2
AP
，
CN
=
BN
=
AN
=
1
2
AB
，∠QMP=∠CND=90°．
∵點D是BP的中點，
∴
BD
=
DP
=
1
2
BP
．
∴
DM
=
DP
+
PM
=
1
2
BP
+
1
2
AP
=
1
2
AB
．
∴DM=CN=AN．
∴AM=DN=QM．
∴△QMD≌△DNC．
∴DQ=DC．

特殊分析：（1）將△APQ繞點A順時針旋轉，當點P落在AB上時，如圖2，探究CD與DQ的數量關系；小明同學的分析如上：填空：①小明判斷△QMD≌△DNC的依據是
（填序號）；
A．SSS
B．SAS
C．AAS
D．ASA
E．HL
②請判斷∠CDQ的度數為
；
一般研討：（2）若將△APQ繞點A在平面內順時針旋轉，如圖3，CD與DQ的數量關系是否發生變化？若變化，請說明理由；若不變化，請證明；
拓展延伸：（3）若
AP
=
4
3
，
BC
=
6
2
，在△AQP繞點A旋轉的過程中，當∠BAP=60°時，請直接寫出線段DQ的長．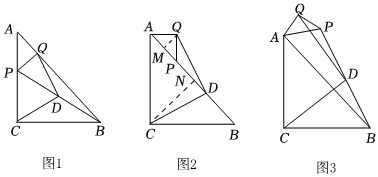

發布：2025/5/22 11:30:2組卷：672引用：4難度：0.2

相關試卷