提出問題：已知平面直角坐標系內，任意一點A，到另外一個點B之間的距離是多少？
問題解決：遇到這種問題，我們可以先從特例入手，最后推理得出結論．
探究一：點A（1，-1）到B（-1，-1）的距離d1=22；
探究二：點A（2，-2）到B（-1，-1）的距離d1=1010；
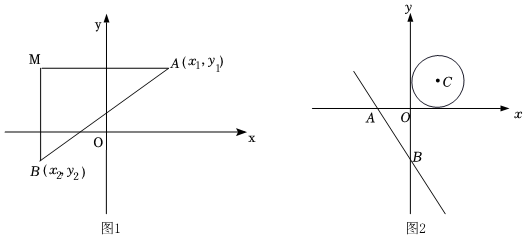
一般規律：（1）如圖1，在平面直角坐標系xOy內，已知A（x1，y1）、B（x2，y2），我們可以表示連接AB，在構造直角三角形，使兩條邊交于M，且∠M=90°，此時AM=x1-x2x1-x2，BM=y1-y2y1-y2，AB=（x1-x2）2+（y1-y2）2（x1-x2）2+（y1-y2）2．
材料補充：已知點P（x0，y0）到直線y=kx+b的距離d2可用公式d2=|kx0-y0+b|1+k2計算．
問題解決：
（2）已知互相平行的直線y=x-2與y=x+b之間的距離是32，試求b的值．
拓展延伸：
拓展一：已知點M（-1，3）與直線y=2x上一點N的距離是3，則△OMN的面積是 52±552±5．
拓展二：如圖2，已知直線y=-43x-4分別交x,y軸于A，B兩點，⊙C是以C（2，2）為圓心，2為半徑的圓，P為⊙C上的動點，試求△PAB面積的最大值．
10
10
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
|
k
x
0
-
y
0
+
b
|
1
+
k
2
2
5
2
±
5
5
2
±
5
4
3
x
-
4
【考點】一次函數綜合題．
【答案】2；；x1-x2；y1-y2；；
10
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
5
2
±
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/2 3:0:2組卷：393引用：2難度：0.3
相似題
-
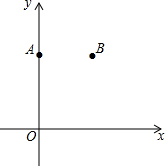1．如圖，在平面直角坐標系xOy中，點A（0，8），點B（6，8）．
（1）只用直尺（沒有刻度）和圓規，求作一個點P，使點P同時滿足下列兩個條件（要求保留作圖痕跡，不必寫出作法）：
①點P到A、B兩點的距離相等；
②點P到∠xOy的兩邊距離相等．
（2）在（1）作出點P后，直接寫出直線PA的解析式．發布：2025/6/24 17:0:1組卷：98引用：3難度：0.1 -
2．如圖，一次函數的圖象分別與x軸、y軸交于點A、B，以線段AB為邊在第一象限內作等腰Rt△ABC，∠BAC=90°．求過B、C兩點直線的解析式．y=-23x+2發布：2025/6/24 15:30:2組卷：2570引用：11難度：0.5 -
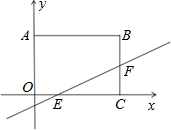3．如圖，在平面直角坐標系中，直線y=x-23與矩形ABCO的邊OC、BC分別交于點E、F，已知OA=3，OC=4，則△CEF的面積是（ ）23發布：2025/6/24 17:30:1組卷：2814引用：31難度：0.9