2023-2024學年山東省青島大學附中八年級（上）期中數學檢測試卷

一、選擇題（本大題共10小題，共30分）

• 1．下列四組數能作為直角三角形三邊長的是（　　）

  A．0.1，0.2，0.3	B．1，1，2
  C．10，24，26	D．32，42，52
  組卷：133引用：4難度：0.7

  解析

• 2．下列各式成立的是（　　）

  A． 1 25 144 =1 5 12	B．（ 3 - 3 ）3=-3
  C． （ - 4 ） 2 =-4	D． 9 =±3
  組卷：300引用：3難度：0.8

  解析

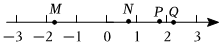• 3．如圖，M、N、P、Q是數軸上的點，那么

  5

  在數軸上對應的點可能是（　　）

  A．點M

  B．點N

  C．點P

  D．點Q
  組卷：529引用：9難度：0.7

  解析

• 4．在平面直角坐標系中，第一象限內的點P（a+3，a）到y軸的距離是5，則a的值為（　　）

  A．-8

  B．2或-8

  C．2

  D．8
  組卷：3184引用：11難度：0.7

  解析

• 5．當a＜-1時，代數式

  |

  1

  +

  a

  |

  -

  a

  2

  的值為（　　）

  A．-1

  B．1

  C．2a+1

  D．-1-2a
  組卷：399引用：6難度：0.7

  解析

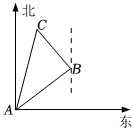• 6．如圖，在“慶國慶，手拉手”活動中，某小組從營地A出發，沿北偏東53°方向走了1200m到達B點，然后再沿北偏西37°方向走了500m到達目的地C點，此時A，C兩點之間的距離為（　　）

  A．1000m

  B．1100m

  C．1200m

  D．1300m
  組卷：403引用：6難度：0.6

  解析

• 7．已知，點A（-2，y₁），B（-1，y₂），C（1，y₃）都在函數y=-2x+b的圖象上，則關于y₁，y₂，y₃的大小關系正確的是（　　）

  A．y3＜y2＜y1

  B．y1＜y2＜y3

  C．y2＜y1＜y3

  D．y3＜y1＜y2
  組卷：123引用：2難度：0.7

  解析

三、解答題（共72分）

• 22．提出問題：已知平面直角坐標系內，任意一點A，到另外一個點B之間的距離是多少？
  問題解決：遇到這種問題，我們可以先從特例入手，最后推理得出結論．
  探究一：點A（1，-1）到B（-1，-1）的距離d₁=

  ；
  探究二：點A（2，-2）到B（-1，-1）的距離d₁=

  ；
  一般規律：（1）如圖1，在平面直角坐標系xOy內，已知A（x₁，y₁）、B（x₂，y₂），我們可以表示連接AB，在構造直角三角形，使兩條邊交于M，且∠M=90°，此時AM=

  ，BM=

  ，AB=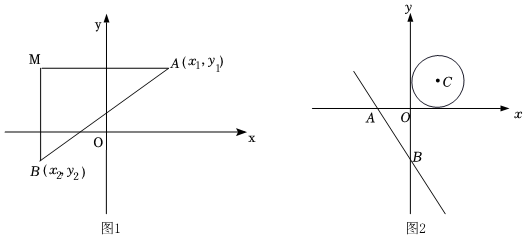

  ．
  
  材料補充：已知點P（x₀，y₀）到直線y=kx+b的距離d₂可用公式d₂=

  |

  k

  x

  0

  -

  y

  0

  +

  b

  |

  1

  +

  k

  2

  計算．
  問題解決：
  （2）已知互相平行的直線y=x-2與y=x+b之間的距離是3

  2

  ，試求b的值．
  拓展延伸：
  拓展一：已知點M（-1，3）與直線y=2x上一點N的距離是3，則△OMN的面積是

  ．
  拓展二：如圖2，已知直線y=-

  4

  3

  x

  -

  4

  分別交x,y軸于A，B兩點，⊙C是以C（2，2）為圓心，2為半徑的圓，P為⊙C上的動點，試求△PAB面積的最大值．
  組卷：390引用：2難度：0.3

  解析

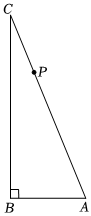• 23．如圖，在△ABC中，∠ABC=90°，AC=13，BA=5，點P從點C出發，以每秒3個單位長度的速度沿折線C-A-B運動．設點P的運動時間為t（t＞0）秒．
  （1）BC=

  ．
  （2）求斜邊AC上的高線長．
  （3）①當P在AB上時，AP的長為

  ，t的取值范圍是

  ．（用含t的代數式表示）
  ②若點P在∠BCA的角平分線上，則t的值為

  ．
  （4）在整個運動過程中，直接寫出△PAB是以AB為一腰的等腰三角形時t的值．
  組卷：871引用：2難度：0.5

  解析