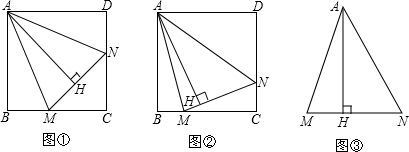
已知,正方形ABCD中,∠MAN=45°,∠MAN繞點A順時針旋轉,它的兩邊分別交CB、DC(或它們的延長線)于點M、N,AH⊥MN于點H.
(1)如圖①,當∠MAN繞點A旋轉到BM=DN時,請你直接寫出AH與AB的數(shù)量關系:AH=ABAH=AB;
(2)如圖②,當∠MAN繞點A旋轉到BM≠DN時,(1)中發(fā)現(xiàn)的AH與AB的數(shù)量關系還成立嗎?如果不成立請寫出理由,如果成立請證明;
(3)如圖③,已知∠MAN=45°,AH⊥MN于點H,且MH=2,NH=3,求AH的長.(可利用(2)得到的結論)
【答案】AH=AB
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網所有,未經書面同意,不得復制發(fā)布。
發(fā)布:2024/7/4 8:0:9組卷:29052引用:48難度:0.1
相似題
-
 1.已知:如圖,E、F分別是正方形ABCD的邊BC、CD上的點,AE、AF分別與對角線BD相交于M、N,若∠EAF=50°,則∠CME+∠CNF=度.發(fā)布:2025/5/28 6:0:2組卷:343引用:7難度:0.7
1.已知:如圖,E、F分別是正方形ABCD的邊BC、CD上的點,AE、AF分別與對角線BD相交于M、N,若∠EAF=50°,則∠CME+∠CNF=度.發(fā)布:2025/5/28 6:0:2組卷:343引用:7難度:0.7 -
2.如圖,將邊長為1的正方形OAPB沿x軸正方向連續(xù)翻轉2012次,點P依次落在點P1,P2,P3,P4,…,P2012的位置,則P2012的橫坐標x2012=( )
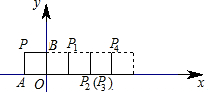
A.2012 B.2011 C.2010 D.2009 發(fā)布:2025/5/28 0:30:1組卷:202引用:2難度:0.9 -
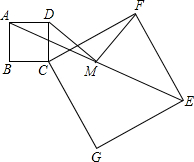 3.如圖,正方形ABCD和正方形CGEF(CG>BC),連接AE,取線段AE的中點M.
3.如圖,正方形ABCD和正方形CGEF(CG>BC),連接AE,取線段AE的中點M.
證明:FM⊥MD,且FM=MD.發(fā)布:2025/5/28 1:30:2組卷:1263引用:2難度:0.1


