小靜同學在手工課上制作了一個容器，經過該容器圓形開口中心點的縱剖面為如圖所示的拋物面形，即剖面邊沿為一條拋物線．經過測量可知該容器的口徑OA=20cm,最大深度為20cm.
（1）在如圖所示的平面直角坐標系中，求出拋物線的表達式．
（2）小靜同學在制作容器的過程中需要將容器分成三層，因此需要制作兩個隔斷板，即如圖所示的EF與GH，要求每層的高度一致，即OA與EF，EF與GH，GH與最低點P之間的距離均相等，同時滿足OA∥EF∥GH．請你根據要求計算隔斷板EF與GH的長度．（結果保留2位小數，參考數據：3≈1.732，6≈2.449）
3
≈
1
.
732
6
≈
2
.
449
【考點】二次函數的應用．
【答案】（1）；
（2）隔斷板EF的長度為16.33cm，GH的長度為11.55cm．
y
=
1
5
x
2
-
4
x
（2）隔斷板EF的長度為16.33cm，GH的長度為11.55cm．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：296引用：2難度：0.1
相似題
-
1．某服裝店銷售某種衣服，其成本為每件60元，當售價為每件100元時，每月可銷售120件．由于疫情的影響，庫存積壓嚴重，為了減少庫存，該服裝店采取降價措施．據市場調查反映：銷售單價每降5元，則每月可多銷售20件．設每件的售價為x元（x為正整數），每月的銷售量為y件．
（1）直接寫出y與x的函數關系式；
（2）當銷售單件降低多少元時，每月獲得的利潤最大，最大利潤是多少？發布：2025/5/23 1:30:2組卷：27引用：1難度：0.5 -
2．某產品每件成本是10元，試銷階段每件產品的售價x（元）與日銷售量y（件）之間的關系如下表：
已知日銷售量y是售價x的一次函數．x（元） 15 20 30 … y（件） 25 20 10 …
（1）求y與x的函數表達式；
（2）當銷售價為多少時，每日的銷售利潤最大？最大利潤是多少？發布：2025/5/23 2:0:6組卷：157引用：3難度：0.6 -
3．某園藝公司計劃投資種植花卉及樹木，根據市場調查與預測，種植樹木的利潤y1（萬元）與投入資金x（萬元）成正比例關系，如圖1所示；種植花卉的利潤y2（萬元）與投入資金x（萬元）成二次函數關系，如圖2所示．
（1）分別求出利潤y1（萬元）與y2（萬元）關于投入資金x（萬元）的函數關系式；
（2）如果該園藝公司以8萬元資金投入種植花卉和樹木，他至少獲得多少利潤？他能獲取的最大利潤是多少？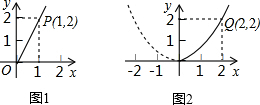
發布：2025/5/23 1:30:2組卷：149引用：5難度：0.7