完全平方公式（a±b）2=a2±2ab+b2進行適當的變形后，可以解決很多的數學問題．
如：若x滿足（9-x）（x-4）=4，求（9-x）2+（x-4）2的值．
解題思路：由（a+b）2=a2+2ab+b2得a2+b2=（a+b）2-2ab,
可設9-x=a,x-4=b,則（9-x）（x-4）=ab=4，a+b=（9-x）+（x-4）=5，
∴（9-x）2+（x-4）2=a2+b2=（a+b）2-2ab=52-2×4=17；
（1）請仿照上面的方法求解下面問題：
①若x滿足（6-x）（x-2）=2，求（6-x）2+（x-2）2的值；
②若x滿足（6+x）（2+x）=5，求（6+x）2+（2+x）2的值；
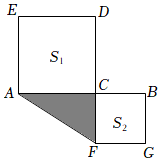
（2）應用上面的解題思路解決問題：如圖，點C是線段AB上的一點，以AC，BC為邊向兩邊作正方形，設AB=8，兩正方形的面積和S1+S2=34，求圖中陰影部分的面積．
【考點】完全平方公式的幾何背景；多項式乘多項式．
【答案】（1）①12；
①26；
（2）7.5．
①26；
（2）7.5．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：314引用：2難度：0.5
相似題
-
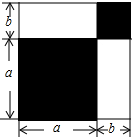1．請認真觀察圖形，解答下列問題：
（1）根據圖中條件，用兩種方法表示兩個陰影圖形的面積的和（只需表示，不必化簡）；
（2）由（1），你能得到怎樣的等量關系？請用等式表示；
（3）如果圖中的a,b（a＞b）滿足a2+b2=53，ab=14，求：
①a+b的值；
②a4-b4的值．發布：2025/6/8 16:0:1組卷：4800引用：21難度：0.3 -
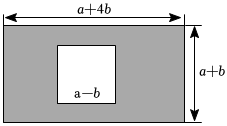2．如圖，現有一塊長為（a+4b）米，寬為（a+b）米的長方形地塊，規劃將陰影部分進行綠化，中間預留部分是邊長為（a-b）米的正方形．
（1）求綠化的面積S（用含a,b的代數式表示，并化簡）；
（2）若a=3，b=2，綠化成本為100元/平方米，則完成綠化共需要多少元？發布：2025/6/8 18:30:1組卷：150引用：3難度：0.5 -
3．【探究】如圖①，從邊長為a的大正方形中剪掉一個邊長為b的小正方形，將陰影部分沿虛線剪開，拼成圖②的長方形．
（1）請你分別表示出這兩個圖形中陰影部分的面積；
（2）比較兩圖的陰影部分面積，可以得到乘法公式：（用字母表示）；
【應用】請應用這個公式完成下列各題：
計算：
（2a+b-c）（2a-b+c）．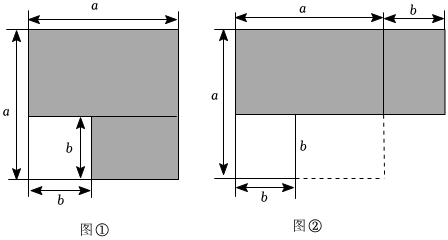
發布：2025/6/8 17:30:2組卷：74引用：1難度：0.6