“化圓為方”是古希臘尺規作圖難題之一．即：求作一個方形，使其面積等于給定圓的面積．這個問題困擾了人類上千年，直到19世紀，該問題被證明僅用直尺和圓規是無法完成的，如果借用一個圓形紙片，我們就可以化圓為方，方法如下：
已知：⊙O（紙片），其半徑為r.
求作：一個正方形，使其面積等于⊙O的面積．
作法：①如圖1，取⊙O的直徑AB，作射線BA，過點A作AB的垂線l；
②如圖2，以點A為圓心，AO長為半徑畫弧交直線l于點C；
③將紙片⊙O沿著直線l向右無滑動地滾動半周，使點A，B分別落在對應的A'，B'處；
④取CB'的中點M，以點M為圓心，MC長為半徑畫半圓，交射線BA于點E；
⑤以AE為邊作正方形AEFG．
正方形AEFG即為所求．
根據上述作圖步驟，完成下列填空：
（1）由①可知，直線l為⊙O的切線，其依據是 經過半徑的外端并且垂直于這條半徑的直線是圓的切線經過半徑的外端并且垂直于這條半徑的直線是圓的切線．
（2）由②③可知，AC=r,AB'=πr,則MC=（π+1）r2（π+1）r2，MA=（π-1）r2（π-1）r2（用含r的代數式表示）．
（3）連接ME，在Rt△AME中，根據AM2+AE2=EM2，可計算得AE2=πr2πr2（用含r的代數式表示）．
由此可得S正方形AEFG=S⊙O．
（
π
+
1
）
r
2
（
π
+
1
）
r
2
（
π
-
1
）
r
2
（
π
-
1
）
r
2
【考點】圓的綜合題．
【答案】經過半徑的外端并且垂直于這條半徑的直線是圓的切線；；；πr2
（
π
+
1
）
r
2
（
π
-
1
）
r
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/10 13:30:2組卷：591引用：5難度：0.4
相似題
-
1．已知：⊙O的半徑為5，點C在直徑AB上，過點C作⊙O的弦DE⊥AB，過點D作直線EB的垂線DF，垂足為點F．
（1）如圖，當AC=2時，求線段EB的長；
（2）當點F是線段EB的中點時，求DF的長；
（3）如果EF=3BF，求線段AC的長．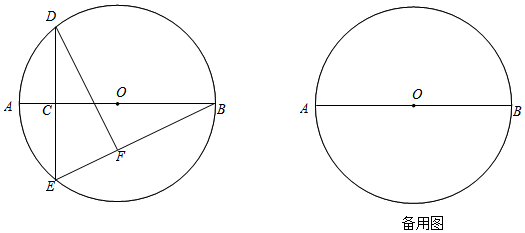
發布：2025/6/11 5:30:2組卷：177引用：2難度：0.2 -
2．如圖，在△ABC中，AB=AC，AO⊥BC于點O，OE⊥AB于點E，以點O為圓心，OE為半徑作半圓，交AO于點F．
（1）求證：AC是⊙O的切線；
（2）若點F是OA的中點，OE=6，求圖中陰影部分的周長；
（3）在（2）的條件下，點P是BC邊上的動點，當PE+PF取最小值時，直接寫出BP的長．發布：2025/6/11 5:30:2組卷：175引用：2難度：0.2 -
3．如圖，已知在Rt△ABC中，∠ACB=90°，AB=5，sinA=
，點P是邊BC上的一點，PE⊥AB，垂足為E，以點P為圓心，PC為半徑的圓與射線PE相交于點Q，線段CQ與邊AB交于點D．45
（1）求AD的長；
（2）設CP=x,△PCQ的面積為y,求y關于x的函數解析式，并寫出定義域；
（3）過點C作CF⊥AB，垂足為F，聯結PF、QF，如果△PQF是以PF為腰的等腰三角形，求CP的長．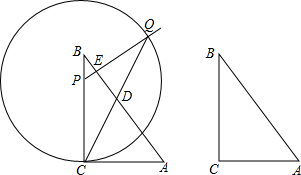
發布：2025/6/11 7:30:2組卷：967引用：5難度：0.1