已知：在正方形ABCD中，∠MAN=45°，∠MAN繞點A順時針旋轉，它的兩邊分別交BC，DC于點M，N，AH⊥MN于點H．
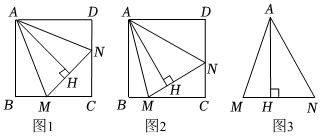
（1）當BM=DN時，AB與AH的數量關系是 AB=AHAB=AH；
（2）當BM≠DN時，AB與AH的數量關系成立嗎？若成立，請證明，若不成立，說明理由；
（3）如圖3，∠MAN=45°，AH⊥MN于點H，MH=2，NH=3，直接寫出AH的長．
【考點】四邊形綜合題．
【答案】AB=AH
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/6 14:0:8組卷：41引用：3難度：0.5
相似題
-
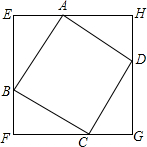1．如圖，正方形ABCD的四個頂點分別在正方形EFGH的四條邊上，我們稱正方形EFGH是正方形ABCD的外接正方形．
探究一：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的2倍？如圖，假設存在正方形EFGH，它的面積是正方形ABCD的2倍．
因為正方形ABCD的面積為1，則正方形EFGH的面積為2，
所以EF=FG=GH=HE=，設EB=x,則BF=2-x,2
∵Rt△AEB≌Rt△BFC
∴BF=AE=-x2
在Rt△AEB中，由勾股定理，得
x2+（-x）2=122
解得，x1=x2=22
∴BE=BF，即點B是EF的中點．
同理，點C，D，A分別是FG，GH，HE的中點．
所以，存在一個外接正方形EFGH，它的面積是正方形ABCD面積的2倍
探究二：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的3倍？（仿照上述方法，完成探究過程）
探究三：已知邊長為1的正方形ABCD，一個外接正方形EFGH，它的面積是正方形ABCD面積的4倍？（填“存在”或“不存在”）
探究四：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的n倍？（n＞2）（仿照上述方法，完成探究過程）發布：2025/6/14 10:0:1組卷：408引用：10難度：0.1 -
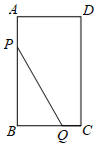2．如圖，矩形ABCD中，AB=4cm,BC=2cm,動點P從點A出發，以2cm/s的速度沿AB向終點B勻速運動；同時動點Q從點B出發，以3cm/s的速度沿BC-CD向終點D勻速運動，連接PQ．設點P的運動時間為t（s），△BPQ的面積為S（cm2）．
（1）當PQ∥BC時，求t的值；
（2）求S與t之間的函數關系式，并寫出自變量t的取值范圍；
（3）當△BPQ的面積是矩形ABCD面積的時，直接寫出t的值．14發布：2025/6/14 10:0:1組卷：85引用：7難度：0.2 -
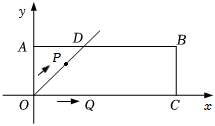3．在平面直角坐標系xOy中，過原點O及點A（0，2）、C（6，0）作矩形OABC，∠AOC的平分線交AB于點D．點P從點O出發，以每秒個單位長度的速度沿射線OD方向移動；同時點Q從點O出發，以每秒2個單位長度的速度沿x軸正方向移動．設移動時間為t秒．2
（1）填空，OP=，OQ=（用含t的代數式表示）；
（2）設△OPQ的面積為S1，△BQC的面積為S2，當t為何值時，S1+S2的值為30．
（3）求當t為何值時，△PQB為直角三角形．發布：2025/6/14 10:0:1組卷：106引用：4難度：0.1