安陽某數學小組就“演繹推理是研究圖形屬性的重要方法”進行了學習，請你一起完成如下任務：
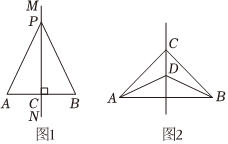
引入：我們已經知道線段是軸對稱圖形，線段的垂直平分線是線段的對稱軸，如圖1，直線MN是線段AB的垂直平分線，P是MN上任意一點，連接PA、PB，將線段AB沿直線MN對折（或對稱），我們發現PA與PB完全重合，由此即有：線段垂直平分線的性質定理：線段垂直平分線上的點到線段兩端的距離相等．
| 任務一：請你根據“引入”，結合圖形把已知和求證補充完整，并寫出證明過程． 已知：如圖1，MN⊥AB，垂足為C， AC=BC AC=BC .點P是直線MN上的任意一點．求證： PA=PB PA=PB ；證明： ∵MN⊥AB， ∴∠PCA=∠PCB=90°， 在△PCA和△PCB中，
∴△PCA≌△PCB（SAS）， ∴PA=PB ∵MN⊥AB， ；∴∠PCA=∠PCB=90°， 在△PCA和△PCB中，
∴△PCA≌△PCB（SAS）， ∴PA=PB |
如圖2，CD是線段AB的垂直平分線，則∠CAD與∠CBD有何關系？請說明理由．
【答案】AC=BC；PA=PB；∵MN⊥AB，
∴∠PCA=∠PCB=90°，
在△PCA和△PCB中，
，
∴△PCA≌△PCB（SAS），
∴PA=PB
∴∠PCA=∠PCB=90°，
在△PCA和△PCB中，
AC = BC |
∠ PCA =∠ PCB |
PC = PC |
∴△PCA≌△PCB（SAS），
∴PA=PB
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/31 18:0:8組卷：36引用：4難度：0.7
相似題
-
1．已知△ABC中，∠ACB=90°，AC=BC=4cm,點P從點A出發，沿AB方向以每秒
cm的速度向終點B運動，同時動點Q從點B出發沿BC方向以每秒1cm的速度向終點C運動，設運動的時間為t秒．2
（1）如圖①，若PQ⊥BC，求t的值；
（2）如圖②，將△PQC沿BC翻折至△P′QC，當t為何值時，四邊形QPCP′為菱形？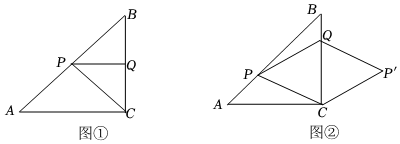
發布：2025/5/31 11:30:1組卷：1347引用：5難度：0.5 -
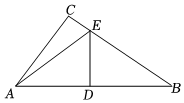2．如圖，在三角形紙片ABC中，AC=6cm,BC=8cm,AB=10cm,折疊紙片使點B與點A重合，DE為折痕，將紙片展開鋪平，連結AE．
（1）判斷△ABC的形狀，并說明理由．
（2）求AE的長．發布：2025/5/31 15:0:2組卷：107引用：4難度：0.5 -
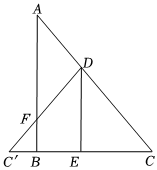3．如圖，在Rt△ABC中，∠ABC=90°，點D在AC上，點E在BC上，將△ABC沿DE折疊，使點C的對應點C'落在EB的延長線上，設DC'交AB于點F，下列結論：①AB∥DE；②∠A=∠C'；③AD=FD，其中正確的結論有（ ）發布：2025/5/31 11:0:1組卷：104引用：2難度：0.4