【新知】
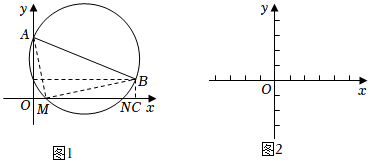
19世紀英國著名文學家和歷史學家卡萊爾給出了一元二次方程x2+bx+c=0的幾何解法：如圖1，在平面直角坐標系中，已知點A（0，1）、B（-b,c），以AB為直徑作⊙P．若⊙P交x軸于點M（m,0）、N（n,0），則m、n為方程x2+bx+c=0的兩個實數根．
【探究】
（1）由勾股定理得，AM2=12+m2，BM2=c2+（-b-m）2，AB2=（1-c）2+b2．在Rt△ABM中，AM2+BM2=AB2所以12+m2+c2+（-b-m）2=（1-c）2+b2．
化簡得：m2+bm+c=0．同理可得：n2+bn+c=0n2+bn+c=0．
所以m、n為方程x2+bx+c=0的兩個實數根．
【運用】
（2）在圖2中的x軸上畫出以方程x2-3x-2=0兩根為橫坐標的點M、N．
（3）已知點A（0，1）、B（6，9），以AB為直徑作⊙C．判斷⊙C與x軸的位置關系，并說明理由．
【拓展】
（4）在平面直角坐標系中，已知兩點A（0，a）、B（-b,c），若以AB為直徑的圓與x軸有兩個交點M、N，則以點M、N的橫坐標為根的一元二次方程是 x2+bx+ac=0x2+bx+ac=0．
【答案】n2+bn+c=0；x2+bx+ac=0
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/6 12:0:8組卷：1877引用：8難度：0.4
相似題
-
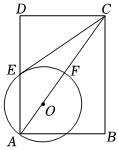1．如圖，矩形ABCD中，點O在對角線AC上，以O為圓心，OA的長為半徑的⊙O與AD、AC分別交于點E、F，且∠ACB=∠DCE．
（1）請判斷直線CE與⊙O的位置關系，并證明你的結論；
（2）當AB：AD=時，直線CB與⊙O相切（只需填出比值即可）．發布：2025/5/21 18:0:1組卷：114引用：1難度：0.6 -
2．已知⊙O的半徑是一元二次方程x2-3x-4=0的一個根，圓心O到直線l的距離d=6，則直線l與⊙O的位置關系是（ ）
發布：2025/5/23 4:0:1組卷：682引用：6難度：0.5 -
3．如圖，在等腰三角形ABC中，AB=AC，D是AB上任意一點，以D為圓心，DB為半徑作⊙D，分別交AB、BC于點E、F，過點F作FG⊥AC，垂足為G．
（1）判斷直線FG與⊙D的位置關系并證明．
（2）若AE=2，BC=3，，求⊙D的半徑．BFCG=2發布：2025/5/22 19:30:1組卷：413引用：2難度：0.5