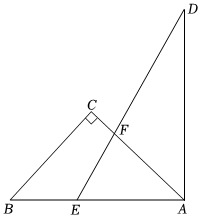
將一副三角板如圖放置，其中點(diǎn)A、E、B在同一直線上，∠C=∠DAE=90°，∠CBA=45°，∠D=30°．
（1）若DE與AC相交于點(diǎn)F，則∠AFE=75°75°；
（2）將圖中的△ADE繞點(diǎn)A以每秒3°的速度逆時(shí)針旋轉(zhuǎn)，設(shè)運(yùn)動(dòng)時(shí)間為t秒．當(dāng)t為何值時(shí)，DE第一次與BC垂直；
（3）△ADE繞點(diǎn)A以每秒3°的速度逆時(shí)針旋轉(zhuǎn)的同時(shí)，△ABC繞點(diǎn)A以每秒2°的速度順時(shí)針，當(dāng)△ABC旋轉(zhuǎn)180°時(shí)，兩個(gè)三角形同時(shí)停止旋轉(zhuǎn)．旋轉(zhuǎn)過程中若射線AE、AB、AC的兩條射線組成的角（大于0°不超過180°）恰好被第三條射線平分，設(shè)運(yùn)動(dòng)時(shí)間為x秒，直接寫出滿足條件的x值．
【考點(diǎn)】三角形綜合題．
【答案】75°
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/21 8:0:10組卷：28引用：1難度：0.3
相似題
-
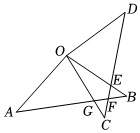1．如圖，△AOB中，OA=OB=6，將△AOB繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)得到△COD．OC與AB交于點(diǎn)G，CD分別交OB、AB于點(diǎn)E、F．
（1）∠A與∠D的數(shù)量關(guān)系是：∠A ∠D；
（2）求證：△AOG≌△DOE；
（3）當(dāng)A，O，D三點(diǎn)共線時(shí)，恰好OB⊥CD，求此時(shí)CD的長．發(fā)布：2025/5/25 10:0:1組卷：82引用：1難度：0.2 -
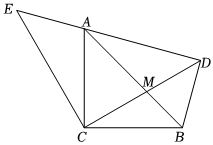2．如圖，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的頂點(diǎn)A在△ECD的斜邊DE上，連接DB．
（1）證明：△EAC≌△DBC；
（2）當(dāng)點(diǎn)A在線段ED上運(yùn)動(dòng)時(shí)，猜想AE、AD和AC之間的關(guān)系，并證明．
（3）在A的運(yùn)動(dòng)過程中，當(dāng)，AE=2時(shí)，求△ACM的面積．AD=6發(fā)布：2025/5/25 8:30:2組卷：376引用：5難度：0.1 -
3．【閱讀理解】
截長補(bǔ)短法，是初中數(shù)學(xué)幾何題中一種輔助線的添加方法．截長就是在長邊上截取一條線段與某一短邊相等，補(bǔ)短是通過在一條短邊上延長一條線段與另一短邊相等，從而解決問題．
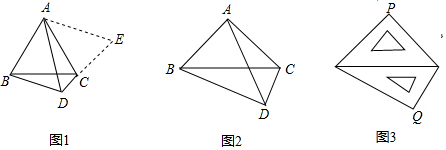
（1）如圖1，△ABC是等邊三角形，點(diǎn)D是邊BC下方一點(diǎn)，∠BDC=120°，探索線段DA、DB、DC之間的數(shù)量關(guān)系．
解題思路：延長DC到點(diǎn)E，使CE=BD，連接AE，根據(jù)∠BAC+∠BDC=180°，可證∠ABD=∠ACE易證得△ABD≌△ACE，得出△ADE是等邊三角形，所以AD=DE，從而探尋線段DA、DB、DC之間的數(shù)量關(guān)系．
根據(jù)上述解題思路，請(qǐng)直接寫出DA、DB、DC之間的數(shù)量關(guān)系是 ；
【拓展延伸】
（2）如圖2，在Rt△ABC中，∠BAC=90°，AB=AC．若點(diǎn)D是邊BC下方一點(diǎn)，∠BDC=90°，探索線段DA、DB、DC之間的數(shù)量關(guān)系，并說明理由；
【知識(shí)應(yīng)用】
（3）如圖3，兩塊斜邊長都為14cm的三角板，把斜邊重疊擺放在一起，則兩塊三角板的直角頂點(diǎn)之間的距離PQ的長為 cm.發(fā)布：2025/5/25 9:0:1組卷：427引用：6難度：0.3