在平面直角坐標系xOy中，M為直線y=x-2上一動點，過點M作拋物線C：x2=y的兩條切線MA，MB，切點分別為A，B，N為AB的中點．
（1）證明：MN⊥x軸；
（2）直線AB是否恒過一定點？若是，求出這個定點的坐標；若不是，請說明理由．
【答案】（1）證明：設切點A（x1，），B（x2，x2），
因為y'=2x，所以切線MA的斜率為2x1，直線MA的方程為：y=2x1（x-x1）+=2x1x-，
設M的坐標為：（t，t-2）
所以-2tx1+t-2=0，
直線MB的斜率為2x2，切線MB的方程為y=2x2x-，
所以M點是方程-2tx2+t-2=0，
所以x1，x2是方程x2-2tx+t-2=0的兩根，x1+x2=2t，
因為N為AB的中點．所以xN==t，
所以M，N的橫坐標相同，
即證MN⊥x軸；
（2）是，定點為定點（，2），理由：
由（1）得yN=（+）==2t2-t+2，
又因為kAB==x1+x2=2t，
所以直線AB的方程為：y-（2t2-t+2）=2t（x-t），即y-2=2t（x-），
所以直線AB恒過一定點（，2）．
x
2
1
因為y'=2x，所以切線MA的斜率為2x1，直線MA的方程為：y=2x1（x-x1）+
x
2
1
x
2
1
設M的坐標為：（t，t-2）
所以
x
2
1
直線MB的斜率為2x2，切線MB的方程為y=2x2x-
x
2
2
所以M點是方程
x
2
2
所以x1，x2是方程x2-2tx+t-2=0的兩根，x1+x2=2t，
因為N為AB的中點．所以xN=
x
1
+
x
2
2
所以M，N的橫坐標相同，
即證MN⊥x軸；
（2）是，定點為定點（
1
2
由（1）得yN=
1
2
x
2
1
x
2
2
（
x
1
+
x
2
）
2
-
2
x
1
x
2
2
又因為kAB=
x
1
2
-
x
2
2
x
1
-
x
2
所以直線AB的方程為：y-（2t2-t+2）=2t（x-t），即y-2=2t（x-
1
2
所以直線AB恒過一定點（
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：110引用：3難度：0.5
相似題
-
1．拋物線x2=4y的焦點為F，準線為l,A，B是拋物線上的兩個動點，且滿足AF⊥BF，P為線段AB的中點，設P在l上的射影為Q，則
的最大值是（ ）|PQ||AB|發布：2024/12/29 5:30:3組卷：460引用：8難度：0.5 -
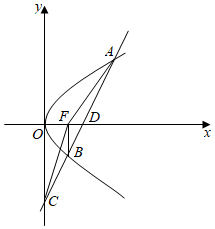2．如圖，設拋物線y2=2px的焦點為F，過x軸上一定點D（2，0）作斜率為2的直線l與拋物線相交于A，B兩點，與y軸交于點C，記△BCF的面積為S1，△ACF的面積為S2，若，則拋物線的標準方程為（ ）S1S2=14發布：2024/12/17 0:0:2組卷：163引用：6難度：0.6 -
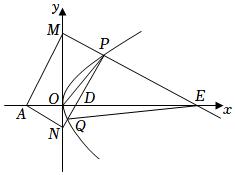3．如圖，已知點P是拋物線C：y2=4x上位于第一象限的點，點A（-2，0），點M，N是y軸上的兩個動點（點M位于x軸上方），滿足PM⊥PN，AM⊥AN，線段PN分別交x軸正半軸、拋物線C于點D，Q，射線MP交x軸正半軸于點E．
（Ⅰ）若四邊形ANPM為矩形，求點P的坐標；
（Ⅱ）記△DOP，△DEQ的面積分別為S1，S2，求S1?S2的最大值．發布：2024/12/29 1:0:8組卷：95引用：2難度：0.4