如圖1，在平面直角坐標系中，直線l1：y=x+1與直線l2：x=-2相交于點D，點A是直線l2上的動點，過點A作AB⊥l1于點B，點C的坐標為（0，3），連接AC，BC．設點A的縱坐標為t,△ABC的面積為s.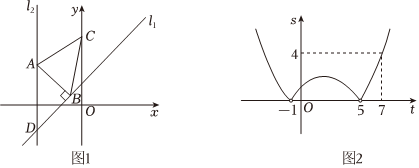
?
（1）當點B的坐標為（-12，12）時，直接寫出t的值；
（2）s關于t的函數解析式為s=14t2+bt-54，t＜-1或t＞5 a（t+1）（t-5），-1＜t＜5
，其圖象如圖2所示，結合圖1、2的信息，求出a與b的值；
（3）在l2上是否存在點A，使得△ABC是直角三角形？若存在，請求出此時點A的坐標和△ABC的面積；若不存在，請說明理由．
（
-
1
2
，
1
2
）
s
=
1 4 t 2 + bt - 5 4 ， t ＜ - 1 或 t ＞ 5 |
a （ t + 1 ） （ t - 5 ） ，- 1 ＜ t ＜ 5 |
【考點】二次函數綜合題．
【答案】（1）t=2；
（2）b=-1，a=-；
（3）點A（-2，1），S△ABC=2或點A（-2，9），S△ABC=10或點A（-2，3），S△ABC=2．
（2）b=-1，a=-
1
4
（3）點A（-2，1），S△ABC=2或點A（-2，9），S△ABC=10或點A（-2，3），S△ABC=2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：54引用：1難度：0.3
相似題
-
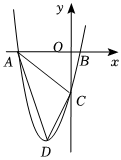1．如圖，拋物線y=x2+4x-5與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C，拋物線的頂點為D．
（1）求△ACD的面積；
（2）在y軸上是否存在點E，使△ADE是直角三角形？若存在，請求出點E的坐標；若不存在，請說明理由．發布：2025/5/24 4:0:7組卷：41引用：1難度：0.3 -
2．拋物線與坐標軸交于A（-1，0），B（4，0），C（0，2）．
（1）求拋物線的解析式；
（2）點D是x軸上的一點，過點D作EF∥AC，交拋物線于E、F，當EF=3AC時，求出點D的坐標；
（3）點D是x軸上的一點，過點D作DE∥AC，交線段BC于E，將△DEB沿DE翻折，得到△DEB′，若△DEB′與△ABC重合部分的面積為S，點D的橫坐標為m,直接寫出S與m的函數關系式并寫出取值范圍．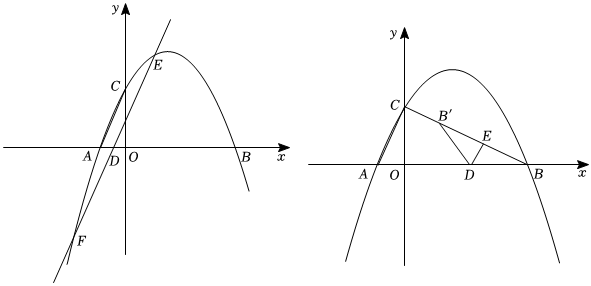
發布：2025/5/24 4:0:7組卷：188引用：1難度：0.1 -
3．如圖，在平面直角坐標系xOy中，正比例函數y=kx（k≠0）和二次函數y=-
x2+bx+3的圖象都經過點A（4，3）和點B，過點A作OA的垂線交x軸于點C．D是線段AB上一點（點D與點A、O、B不重合），E是射線AC上一點，且AE=OD，連接DE，過點D作x軸的垂線交拋物線于點F，以DE、DF為鄰邊作?DEGF．14
（1）填空：k=，b=；
（2）設點D的橫坐標是t（t＞0），連接EF．若∠FGE=∠DFE，求t的值；
（3）過點F作AB的垂線交線段DE于點P，若S△DFP=S?DEGF，求OD的長．13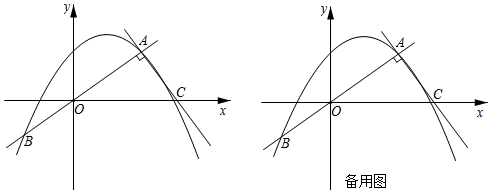
發布：2025/5/24 4:0:7組卷：3463引用：4難度：0.1