問題提出
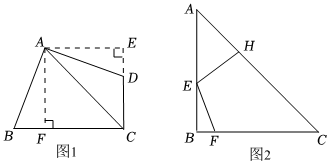
（1）如圖1，在四邊形ABCD中，∠BAD=∠BCD=90°，AB=AD，AC=4，圖中已作出輔助線，請你按照這種思路，求出四邊形ABCD的面積；
問題解決
（2）如圖2，等腰△ABC是某公園的一塊空地，AB=12（2+1） m，∠B=90°．園區管理員想要在這塊空地內修建兩條觀光小路EH和EF（小路寬度不計，F在BC邊上，H在AC邊上），將其分成三個區域種植不同的花卉，且在AB邊上的點E處修建一個涼亭．根據實際需要，AE=122 m，∠HEF=105°，并且要求四邊形EFCH的面積盡可能大．請問，是否存在滿足條件的四邊形EFCH？若存在，求四邊形EFCH的面積最大值；若不存在，請說明理由．
AB
=
12
（
2
+
1
）
m
AE
=
12
2
m
【考點】二次函數的應用．
【答案】（1）8；
（2）．
（2）
144
（
3
+
2
-
1
）
m
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/10 8:0:9組卷：275引用：3難度：0.5
相似題
-
1．某超市經銷種商品，每千克成本為40元，經試銷發現，該種商品的每天銷售量y（千克）與銷售單價x（元/千克）滿足一次函數關系，其每天銷售單價，銷售量的四組對應值如表所示：
（1）求y（千克）與x（元/千克）之間的函數表達式；銷售單價x（元/千克） 45 50 55 60 銷售量y（千克） 110 100 90 80
（2）為保證某天獲得1600元的銷售利潤，則該天的銷售單價x應定為多少？
（3）當銷售單價x定為多少時，才能使當天的銷售利潤最大？最大利潤是多少？發布：2025/5/29 21:0:2組卷：30引用：3難度：0.2 -
2．如圖，若被擊打的小球距離地面的高度h（m）與被擊打后經過的時間t（s）的關系為h=24t-4t2，則小球從被擊打到落地所用的時間為 ．發布：2025/5/29 21:0:2組卷：193引用：3難度：0.6 -
3．如圖，在某場足球比賽中，球員甲從球門底部中心點O的正前方10m處起腳射門，足球沿拋物線飛向球門中心線；當足球飛離地面高度為3m時達到最高點，此時足球飛行的水平距離為6m.已知球門的橫梁高OA為2.44m.
（1）在如圖所示的平面直角坐標系中，問此飛行足球能否進球門？（不計其它情況）
（2）守門員乙站在距離球門2m處，他跳起時手的最大摸高為2.52m,他能阻止球員甲的此次射門嗎？如果不能，他至少后退多遠才能阻止球員甲的射門？發布：2025/5/29 20:30:1組卷：2902引用：15難度：0.5