 在《二元一次方程組》“數學活動”的學習中,小華同學對二元一次方程2x+y=2的解與平面直角坐標系內點的對應關系做了如下探究,請將小華同學的探究過程補充完整.
在《二元一次方程組》“數學活動”的學習中,小華同學對二元一次方程2x+y=2的解與平面直角坐標系內點的對應關系做了如下探究,請將小華同學的探究過程補充完整.
(1)補全下列表格,使上下每對x,y的值都是方程2x+y=2的解.
| x | -1 | m | 1 | 2 | 3 |
| y | 4 | 2 | 0 | -2 | n |
0
0
,n=-4
-4
;(2)如果將表中的各組解表示為點的坐標(x,y)的形式,例如,方程2x+y=2的解
x = - 1 |
y = 4 |
(3)觀察這些點,猜想方程2x+y=2的所有解的對應點所組成的圖形是
一條直線
一條直線
;(4)若關于x,y的二元一次方程2x+y=2,ax+by=1的所有解所組成的圖形的交點坐標為(1,0),則二元一次方程組
2 x + y = 2 |
ax + by = 1 |
x = 1 |
y = 0 |
x = 1 |
y = 0 |
【答案】0;-4;一條直線;
x = 1 |
y = 0 |
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/7 9:30:1組卷:95引用:2難度:0.5
相似題
-
1.已知關于a,b的方程組
的解是3a+b=ma+bm=n,則直線y=mx+n不經過( )a=-1b=1A.第一象限 B.第二象限 C.第三象限 D.第四象限 發布:2025/6/8 14:30:2組卷:399引用:4難度:0.7 -
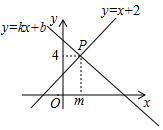 2.如圖,一次函數y=kx+b與y=x+2的圖象相交于點P(m,4),則方程組的解是( )y=x+2y=kx+b
2.如圖,一次函數y=kx+b與y=x+2的圖象相交于點P(m,4),則方程組的解是( )y=x+2y=kx+bA. x=2y=4B. x=-2y=4C. x=4y=2D. x=4y=-2發布:2025/6/7 21:30:1組卷:1133引用:10難度:0.7 -
 3.圖中兩條直線l1和l2的交點坐標可以看作方程組 的解.發布:2025/6/8 10:30:2組卷:623引用:2難度:0.5
3.圖中兩條直線l1和l2的交點坐標可以看作方程組 的解.發布:2025/6/8 10:30:2組卷:623引用:2難度:0.5


