（1）【問題背景】如圖1，在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，∠BAD=120°，E，F(xiàn)分別是BC，CD上的點(diǎn)，∠EAF=60°，求證：BE+FD=EF．
小亮同學(xué)認(rèn)為延長(zhǎng)FD到點(diǎn)G，使DG=BE，連結(jié)AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，即可得證，并寫出了以下的思維框圖：
請(qǐng)問：小亮同學(xué)②處用到的判定依據(jù)是 CC．
A．SSS
B．ASA
C．SAS
D．AAS
（2）【探索延伸】如圖2，在四邊形ABCD中，AB=AD，∠B+∠D=180°，E，F(xiàn)分別是BC，CD上的點(diǎn)，∠EAF=12∠BAD，上述結(jié)論是否仍然成立？請(qǐng)說明理由．
（3）【結(jié)論運(yùn)用】在平面直角坐標(biāo)系中，正方形OABC如圖3放置，O是坐標(biāo)原點(diǎn)，點(diǎn)A、點(diǎn)C分別在y軸和x軸上，E，F(xiàn)分別是OC，BC上的點(diǎn)，∠EAF=45°，若點(diǎn)F的坐標(biāo)為（m,3），EF=5，試求出點(diǎn)E的坐標(biāo)（可直接運(yùn)用背景結(jié)論）．
∠
EAF
=
1
2
∠
BAD
【考點(diǎn)】四邊形綜合題．
【答案】C
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/1 2:30:1組卷：90引用：1難度：0.1
相似題
-
1．問題背景
定義：若兩個(gè)等腰三角形有公共底邊，且兩個(gè)頂角的和是180°，則稱這兩個(gè)三角形是關(guān)于這條底邊的互補(bǔ)三角形．如圖1，四邊形ABCD中，BC是一條對(duì)角線，AB=AC，DB=DC，且∠A+∠D=180°，則△ABC與△DBC是關(guān)于BC的互補(bǔ)三角形．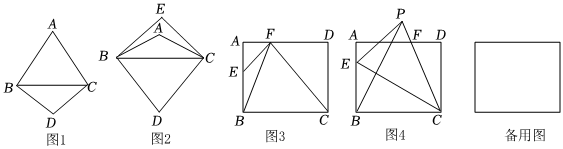
（1）初步思考：如圖2，在△ABC中，AB=AC，∠ABC=30°，D、E為△ABC外兩點(diǎn)，EB=EC，∠EBC=45°，△DBC為等邊三角形．則△ABC關(guān)于BC的互補(bǔ)三角形是 ，并說明理由．
（2）實(shí)踐應(yīng)用：如圖3，在長(zhǎng)方形ABCD中，AB=8，AD=10．點(diǎn)E在AB邊上，點(diǎn)F在AD邊上，若△BEF與△BCF是關(guān)于BF互補(bǔ)三角形，試求AE的長(zhǎng)．
（3）思維探究：如圖4，在長(zhǎng)方形ABCD中，AB=8，AD=10．點(diǎn)E是線段AB上的動(dòng)點(diǎn)，點(diǎn)P是平面內(nèi)一點(diǎn)，△BEP與△BCP是關(guān)于BP的互補(bǔ)三角形，直線CP與直線AD交于點(diǎn)F．在點(diǎn)E運(yùn)動(dòng)過程中，線段BE與線段AF的長(zhǎng)度是否會(huì)相等？若相等，請(qǐng)直接寫出AE的長(zhǎng)；若不相等，請(qǐng)說明理由．發(fā)布：2025/6/2 17:30:1組卷：304引用：5難度：0.3 -
2．如圖1，在正方形ABCD中，M、N分別為邊AB、AD上的點(diǎn)，連接CM、CN，且CM=CN．
（1）求證：△BMC≌△DNC；
（2）如圖2，若P是邊BC上的點(diǎn)，且NP⊥CM于O，連接OA，求證：OM+ON=OA；2
（3）如圖3，在滿足（2）的條件下，過O作OQ⊥BC于Q，若AM=2BM，求的值．OQCD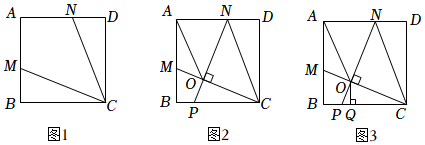
發(fā)布：2025/6/2 16:0:1組卷：755引用：4難度：0.4 -
3．如圖，在平面直角坐標(biāo)系中，已知矩形OABC的頂點(diǎn)A在x軸上，頂點(diǎn)C在y軸上，OA=8，OC=4，點(diǎn)P為對(duì)角線AC上一動(dòng)點(diǎn)，過點(diǎn)P作PQ⊥PB，PQ交x軸于點(diǎn)Q．
（1）tan∠ACB=；
（2）在點(diǎn)P從點(diǎn)C運(yùn)動(dòng)到點(diǎn)A的過程中，的值是否發(fā)生變化？如果變化，請(qǐng)求出其變化范圍；如果不變，請(qǐng)求出其值；PQPB
（3）若將△QAB沿直線BQ折疊后，點(diǎn)A與點(diǎn)P重合，求PC的長(zhǎng)．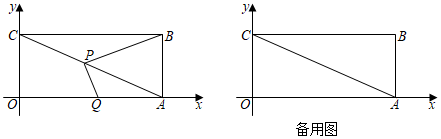
發(fā)布：2025/6/2 13:30:2組卷：504引用：2難度：0.4