【問題情境】
在一次數學興趣小組活動中，小昕同學將一大一小兩個三角板按照如圖1所示的方式擺放．其中∠ACB=∠DEB=90°，∠B=30°，BE=AC=3．
【問題探究】
小昕同學將三角板DEB繞點B按順時針方向旋轉．
（1）如圖2，當點E落在邊AB上時，延長DE交BC于點F，求BF的長．
（2）若點C、E、D在同一條直線上，求點D到直線BC的距離．
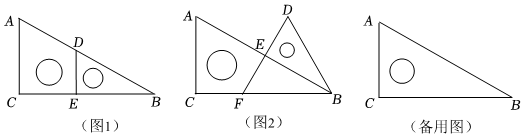
（3）連接DC，取DC的中點G，三角板DEB由初始位置（圖1），旋轉到點C、B、D首次在同一條直線上（如圖3），求點G所經過的路徑長．
（4）如圖4，G為DC的中點，則在旋轉過程中，點G到直線AB的距離的最大值是 734734．
7
3
4
7
3
4
【考點】幾何變換綜合題．
【答案】
7
3
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：3846引用：6難度：0.3
相似題
-
1．已知點M，N是直線l上自左向右的兩點，且MN=8，點P是MN的中點，點Q是直線l上一點（不與點M，N重合），直線m經過點Q，MA⊥直線m于點A，NB⊥直線m于點B，連接PA，PB．
（1）如圖1，當點Q在點P，N之間時，求證：PA=PB；
（2）如圖2，當點Q在點N的右側時，若PN=2NQ，且∠AQM=30°，求AB和AP的長度．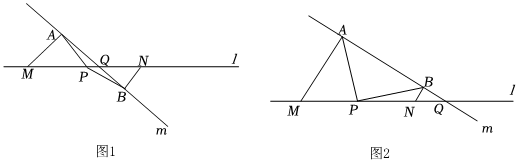
發布：2025/5/22 17:0:1組卷：74引用：1難度：0.3 -
2．如圖1，四邊形ABCD中，∠BCD=90°，AC=AD，AF⊥CD于點F，交BD于點E，∠ABD=2∠BDC．
（1）判斷線段AE與BC的關系，并說明理由；
（2）若∠BDC=30°，求∠ACD的度數；
（3）如圖2，在（2）的條件下，線段BD與AC交于點O，點G是△BCE內一點，∠CGE=90°，GE=3，將△CGE繞著點C逆時針旋轉60°得△CMH，E點對應點為M，G點的對應點為H，且點O，G，H在一條直線上直接寫出OG+OH的值．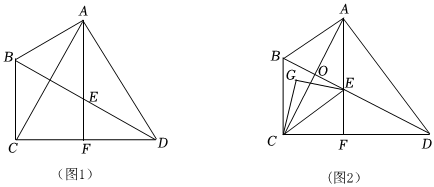
發布：2025/5/22 19:0:1組卷：523引用：1難度：0.2 -
3．如圖1，在Rt△ABC中，∠BAC=90°，∠ACB=60°，AC=1，點A1，B1為邊AC，BC的中點，連接A1B1，將△A1B1C繞點C逆時針旋轉α（0°≤α≤360°）．
（1）如圖1，當α=0°時，=；BB1，AA1所在直線相交所成的較小夾角的度數是 ；BB1AA1
（2）將△A1B1C繞點C逆時針旋轉至圖2所示位置時，（1）中結論是否仍然成立？若成立，請給出證明；若不成立，請說明理由；
（3）當△A1B1C繞點C逆時針旋轉過程中，請直接寫出S△ABA1的最大值，S△ABA1=．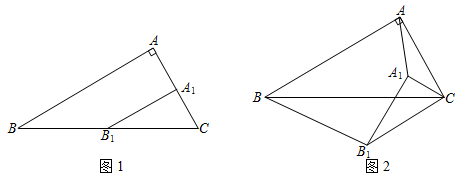
發布：2025/5/22 19:0:1組卷：432引用：3難度：0.4