“工藝折紙”是一種把紙張折成各種不同形狀物品的藝術活動,在我國源遠流長.某些折紙活動蘊含豐富的數學內容,例如:用一張圓形紙片,按如下步驟折紙(如圖)
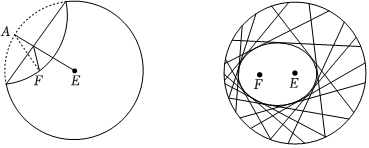
步驟1:設圓心是E,在圓內異于圓心處取一點,標記為F;
步驟2:把紙片折疊,使圓周正好通過點F;
步驟3:把紙片展開,并留下一道折痕;
步驟4:不停重復步驟2和3,就能得到越來越多的折痕.已知這些折痕所圍成的圖形是一個橢圓.若取半徑為4的圓形紙片,設定點F到圓心E的距離為23,按上述方法折紙.
(1)以點F、E所在的直線為x軸,建立適當的坐標系,求折痕圍成的橢圓C的標準方程;
(2)設橢圓C的下頂點為D,過點D作兩條互相垂直的直線l1,l2,這兩條直線與橢圓C的另一個交點分別為M,N.設l的斜率為k(k≠0),△DMN的面積為S,當S|k|>169時,求k的取值范圍.
2
3
S
|
k
|
>
16
9
【考點】直線與圓錐曲線的綜合.
【答案】(1)橢圓C的方程為;
(2)k的取值范圍為(-,0)∪(0,).
x
2
4
+
y
2
=
1
(2)k的取值范圍為(-
2
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/10 2:0:9組卷:67引用:3難度:0.5
相似題
-
1.點P在以F1,F2為焦點的雙曲線
(a>0,b>0)上,已知PF1⊥PF2,|PF1|=2|PF2|,O為坐標原點.E:x2a2-y2b2=1
(Ⅰ)求雙曲線的離心率e;
(Ⅱ)過點P作直線分別與雙曲線漸近線相交于P1,P2兩點,且,OP1?OP2=-274,求雙曲線E的方程;2PP1+PP2=0
(Ⅲ)若過點Q(m,0)(m為非零常數)的直線l與(2)中雙曲線E相交于不同于雙曲線頂點的兩點M、N,且(λ為非零常數),問在x軸上是否存在定點G,使MQ=λQN?若存在,求出所有這種定點G的坐標;若不存在,請說明理由.F1F2⊥(GM-λGN)發布:2024/12/29 10:0:1組卷:72引用:5難度:0.7 -
2.已知兩個定點坐標分別是F1(-3,0),F2(3,0),曲線C上一點任意一點到兩定點的距離之差的絕對值等于2
.5
(1)求曲線C的方程;
(2)過F1(-3,0)引一條傾斜角為45°的直線與曲線C相交于A、B兩點,求△ABF2的面積.發布:2024/12/29 10:30:1組卷:102引用:1難度:0.9 -
3.若過點(0,-1)的直線l與拋物線y2=2x有且只有一個交點,則這樣的直線有( )條.
A.1 B.2 C.3 D.4 發布:2024/12/29 10:30:1組卷:26引用:5難度:0.7


