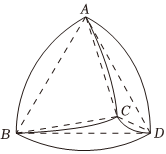
勒洛四面體是一個(gè)非常神奇的“四面體”，它能在兩個(gè)平行平面間自由轉(zhuǎn)動(dòng)，并且始終保持與兩平面都接觸，因此它能像球一樣來回滾動(dòng)．勒洛四面體是以正四面體的四個(gè)頂點(diǎn)為球心，以正四面體的棱長為半徑的四個(gè)球的公共部分，如圖所示，若正四面體ABCD的棱長為a.
①能夠容納勒洛四面體的正方體的棱長的最小值為a
②勒洛四面體能夠容納的最大球的半徑為（1-32）a
③勒洛四面體中過A、B、C三點(diǎn)的截面面積為14（2π-3）a2
④勒洛四面體的體積V∈（212a3，6π8a3）
上述命題中正確的是 ①④①④．
（
1
-
3
2
）
a
1
4
（
2
π
-
3
）
a
2
V
∈
（
2
12
a
3
，
6
π
8
a
3
）
【考點(diǎn)】棱柱、棱錐、棱臺(tái)的體積；命題的真假判斷與應(yīng)用．
【答案】①④
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/10/3 10:0:1組卷：130引用：1難度：0.2
相似題
-
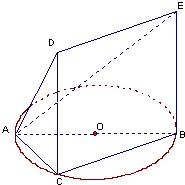1．如圖，△ABC內(nèi)接于圓O，AB是圓O的直徑，AB=2，BC=1，設(shè)AE與平面ABC所成的角為θ，且tanθ=，四邊形DCBE為平行四邊形，DC⊥平面ABC．32
（1）求三棱錐C-ABE的體積；
（2）證明：平面ACD⊥平面ADE；
（3）在CD上是否存在一點(diǎn)M，使得MO∥平面ADE？證明你的結(jié)論．發(fā)布：2025/1/20 8:0:1組卷：95引用：3難度：0.1 -
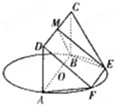2．如圖，AB為圓O的直徑，點(diǎn)E、F在圓O上，AB∥EF，矩形ABCD的邊BC垂直于圓O所在的平面，且AB=2，AD=EF=1．
（Ⅰ）設(shè)CD的中點(diǎn)為M，求證：EM∥平面DAF；
（Ⅱ）求三棱錐B-CME的體積．發(fā)布：2025/1/20 8:0:1組卷：16引用：1難度：0.5 -
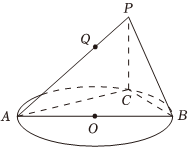3．如圖所示，AB為圓O的直徑，PC⊥平面ABC，Q在線段PA上．
（1）求證：平面BCQ⊥平面ACQ；
（2）若Q為靠近P的一個(gè)三等分點(diǎn)，PC=BC=1，，求VP-BCQ的值．AC=22發(fā)布：2025/1/20 8:0:1組卷：38引用：3難度：0.6