如圖1，是一個長為4a、寬為b的長方形，沿圖中虛線用剪刀平均分成四塊小長方形，然后用四塊小長方形拼成一個“回形”正方形（如圖2）．
（1）觀察圖2，請你寫出（a+b）2、（a-b）2、ab之間的等量關(guān)系是 （b+a）2=（b-a）2+4ab（b+a）2=（b-a）2+4ab；
根據(jù)（1）中的結(jié)論，解決下列問題：
（2）若x-y=5，xy=6，則x+y=7或-77或-7；
（3）設(shè)A=x-2y-34，B=x+2y-3，求（A-B）2-（A+B）2的結(jié)果；
（4）若（2023-m）2+（m-2021）2=9，求（2023-m）（m-2021）=-52-52．
x
-
2
y
-
3
4
5
2
5
2
【考點】完全平方公式的幾何背景．
【答案】（b+a）2=（b-a）2+4ab；7或-7；-
5
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/13 8:0:9組卷：146引用：1難度：0.6
相似題
-
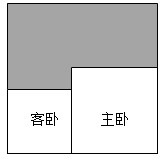1．如圖所示的是正方形的房屋結(jié)構(gòu)平面圖，其中主臥與客臥都是正方形，其面積之和比其余面積（陰影部分）多6.25m2，則主臥與客臥的周長差是（ ）發(fā)布：2025/1/1 6:30:3組卷：212引用：4難度：0.6 -
2．靈活運用完全平方公式（a±b）2=a2±2ab+b2可以解決許多數(shù)學(xué)問題．
例如：已知a-b=3，ab=1，求a2+b2的值．
解：∵a-b=3，ab=1，∴（a-b）2=9，2ab=2，∴a2-2ab+b2=9，∴a2-2+b2=9，∴a2+b2=9+2=11．
請根據(jù)以上材料，解答下列問題．
（1）若a2+b2與2ab-4互為相反數(shù)，求a+b的值．
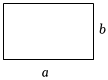
（2）如圖，矩形的長為a,寬為b,周長為14，面積為8，求a2+b2的值．發(fā)布：2025/5/23 21:0:1組卷：435引用：4難度：0.6 -
3．如圖，一個正方形被分成兩個正方形和兩個一模一樣的矩形，請根據(jù)圖形，寫出一個含有a,b的正確的等式．發(fā)布：2025/5/25 0:30:1組卷：573引用：8難度：0.5