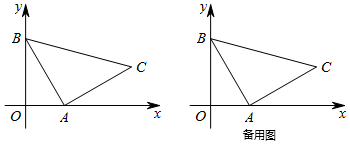
如圖，在平面直角坐標系中，△ABC為等腰直角三角形，∠BAC=90°，AB=AC，頂點A（a,0），B（0，b）分別在x軸，y軸上，且滿足a-2+（23-b）2=0．
（1）a=22，b=2323；
（2）求點C的坐標；
（3）在平面直角坐標系中找一點D，使得點A，B，C，D組成的四邊形為平行四邊形．
a
-
2
+
（
2
3
-
b
）
2
=
0
3
3
【答案】2；2
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：545引用：1難度：0.5
相似題
-
1．一個四邊形，對于下列條件：①一組對邊平行，一組對角相等；②一組對邊平行，一條對角線被另一條對角線平分；③一組對邊相等，一條對角線被另一條對角線平分；④兩組對角的平分線分別平行，不能判定為平行四邊形的是（ ）
發布：2025/5/27 15:0:2組卷：723引用：16難度：0.7 -
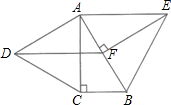2．如圖，分別以Rt△ABC的直角邊AC及斜邊AB向外作等邊△ACD、等邊△ABE．已知∠BAC=30°，EF⊥AB，垂足為F，連接DF．求證：四邊形ADFE是平行四邊形．發布：2025/5/28 7:30:2組卷：1732引用：4難度：0.7 -
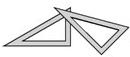3．如圖，有兩塊全等的含30°角的三角板拼成形狀不同的平行四邊形，最多可以拼成（ ）發布：2025/5/27 3:30:1組卷：385引用：26難度：0.9